题目内容
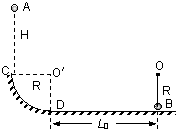 如图所示,半径为R的 1/4光滑圆弧轨道最低点D与水平面相切,在D点右侧L0=4R处用长为R的细绳将质量为m的小球B(可视为质点)悬挂于O点,小球B的下端恰好与水平面接触,质量为m的小球A(可视为质点)自圆弧轨道C的正上方H高处由静止释放,恰好从圆弧轨道的C点切入圆弧轨道,已知小球A与水平面间的动摩擦因数μ=0.5,细绳的最大张力Fm=7mg,重力加速度为g,试求:(1)若H=R,小球A到达圆弧轨道最低点D时所受轨道的支持力;
如图所示,半径为R的 1/4光滑圆弧轨道最低点D与水平面相切,在D点右侧L0=4R处用长为R的细绳将质量为m的小球B(可视为质点)悬挂于O点,小球B的下端恰好与水平面接触,质量为m的小球A(可视为质点)自圆弧轨道C的正上方H高处由静止释放,恰好从圆弧轨道的C点切入圆弧轨道,已知小球A与水平面间的动摩擦因数μ=0.5,细绳的最大张力Fm=7mg,重力加速度为g,试求:(1)若H=R,小球A到达圆弧轨道最低点D时所受轨道的支持力;(2)试讨论H在什么范围内,小球A与B发生弹性碰撞后细绳始终处于拉直状态.
分析:(1)小球开始下落一直到D的过程中,只有重力做功,由机械能守恒定律可以求出到达D点的速度,由牛顿第二定律可以求出支持力;
(2)应用动量守恒定律、动能定理、牛顿第二定律求出H的范围.
(2)应用动量守恒定律、动能定理、牛顿第二定律求出H的范围.
解答:解:(1)设小球A运动到圆弧轨道最低点D时速度为v0,
则由机械能守恒定律有:
mv02=mg(H+R) ①
圆弧轨道最低点,由牛顿第二定律可得:N-mg=m
②
解得:N=5mg ③;
(2)设A与B碰前速度为vA,碰后A的速度为vA′,B的速度为vB,
A与B碰撞过程,由动量守恒定律得:mvA=mvA′+mvB ④
由机械能守恒定律得:
mvA2=
mvA′2+
mvB2 ⑤,
A在水平面上滑行过程,由动能定理得:-μmgL0=
mvA2-
mv02 ⑥
A、若碰后B能在竖直平面内做完整的圆周运动,则细绳始终处于拉直状态,
设小球B在最高处速度为vB′,则在最高处有:mg≤m
⑦
小球B从最低点到最高点:
mvB2=
mvB′2+mg?2R ⑧,
小球B在最低点时细绳受力最大,Fm-mg≥m
⑨
联立①④⑤⑥⑦⑧⑨解得:3.5R≤H≤4R ⑩,
B、若A与B碰后B摆动的最大高度小于R,则细绳始终处于拉直状态,则
根据机械能守恒得:
mvB2≤mgR (11),
要保证A与B能发生碰撞,vA>0,(12)
联立①④⑤⑥(11)(12)解得:R<H≤2R;
答:(1)若H=R,小球A到达圆弧轨道最低点D时所受轨道的支持力为5mg;
(2)当3.5R≤H≤4R或R<H≤2R时,小球A与B发生弹性碰撞后细绳始终处于拉直状态.
则由机械能守恒定律有:
| 1 |
| 2 |
圆弧轨道最低点,由牛顿第二定律可得:N-mg=m
| ||
| R |
解得:N=5mg ③;
(2)设A与B碰前速度为vA,碰后A的速度为vA′,B的速度为vB,
A与B碰撞过程,由动量守恒定律得:mvA=mvA′+mvB ④
由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A在水平面上滑行过程,由动能定理得:-μmgL0=
| 1 |
| 2 |
| 1 |
| 2 |
A、若碰后B能在竖直平面内做完整的圆周运动,则细绳始终处于拉直状态,
设小球B在最高处速度为vB′,则在最高处有:mg≤m
| ||
| R |
小球B从最低点到最高点:
| 1 |
| 2 |
| 1 |
| 2 |
小球B在最低点时细绳受力最大,Fm-mg≥m
| ||
| R |
联立①④⑤⑥⑦⑧⑨解得:3.5R≤H≤4R ⑩,
B、若A与B碰后B摆动的最大高度小于R,则细绳始终处于拉直状态,则
根据机械能守恒得:
| 1 |
| 2 |
要保证A与B能发生碰撞,vA>0,(12)
联立①④⑤⑥(11)(12)解得:R<H≤2R;
答:(1)若H=R,小球A到达圆弧轨道最低点D时所受轨道的支持力为5mg;
(2)当3.5R≤H≤4R或R<H≤2R时,小球A与B发生弹性碰撞后细绳始终处于拉直状态.
点评:分析清楚运动过程是正确解题的关键,要对绳子拉直进行讨论,不要漏解.

练习册系列答案
相关题目
 如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求:
如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求: 如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点.
如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点. 如图所示,半径为R的
如图所示,半径为R的 如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )
如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )