题目内容
10．
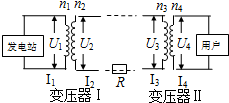远距离输电的原理图如图所示，变压器Ⅰ和变压器Ⅱ的原、副线圈的匝数分别为n1、n2和n3、n4，电压分别为U1、U2和U3、U4，电流分别为I1、I2和I3、I4，输电线上的电阻为R．变压器为理想变压器，下列说法正确的是（ ）| A． | I1=I4 | B． | I2=$\frac{{U}_{2}}{R}$ | ||
| C． | 变压器Ⅰ是升压变压器 | D． | U1I1=U4I4 |
分析 变压器电压之比等于匝数之比；电流之比等于匝数的反比；在远距离输电中，输电导线上功率有损耗．
解答 解：A、升压变压器电流之比等于匝数的反比，故有：$\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{2}}{{n}_{1}}$；
同理$\frac{{I}_{3}}{{I}_{4}}$=$\frac{{n}_{4}}{{n}_{3}}$，故A错误；
B、U2是输电导线及降压变压器两端的电压，不能只对导线由欧姆定律求电流；故B错误；
C、发电厂升压后减小电流，所以压器Ⅰ是升压变压器，故C正确；
D、由于导线通电发热导致能量损失，所以U1I1＞U4I4，故D错误；
故选：C．
点评 理想变压器的输入功率与输出功率相等，且没有漏磁现象．远距离输电，由于导线通电发热导致能量损失，所以通过提高输送电压，从而实现降低电损
练习册系列答案
津桥教育计算小状元系列答案
相关题目
1．
如图所示，带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内，恰好沿下板的边缘飞出，已知板长为L，板间的距离为d，板间电压为U，带电粒子的电荷量为q，粒子通过平行金属板的时间为t，（不计粒子的重力），则（ ）
如图所示，带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内，恰好沿下板的边缘飞出，已知板长为L，板间的距离为d，板间电压为U，带电粒子的电荷量为q，粒子通过平行金属板的时间为t，（不计粒子的重力），则（ ）| A． | 在前$\frac{t}{2}$时间内，电场力对粒子做的功为$\frac{{U}_{q}}{4}$ | |
| B． | 在后$\frac{t}{2}$时间内，电场力对粒子做的功为$\frac{3{U}_{q}}{8}$ | |
| C． | 在粒子下落前$\frac{d}{4}$和后$\frac{d}{4}$的过程中，电场力做功之比为1：2 | |
| D． | 在粒子下落前$\frac{d}{4}$和后$\frac{d}{4}$的过程中，电场力做功之比为2：1 |
18．桌子静置于水平地面上，则（ ）
| A． | 桌子所受的重力与地面的支持力等大反向，是一对作用力和反作用力 | |
| B． | 因桌子静止在地面上，所以桌子的重力与桌子对地面的压力是相互作用力 | |
| C． | 桌子所受的重力大小等于地面对桌子的支持力，这两个力是一对平衡力 | |
| D． | 桌子对地面的压力就是桌子的重力，这两个力是不同性质的力 |
2．
在距离地面高为H的桌面上，以速度v水平抛出质量为m的小球，如图所示，设地面处物体重力势能为零，空气阻力不计，那么，当小球运动到距离地面高为h的A点时，下列说法正确的是（ ）
在距离地面高为H的桌面上，以速度v水平抛出质量为m的小球，如图所示，设地面处物体重力势能为零，空气阻力不计，那么，当小球运动到距离地面高为h的A点时，下列说法正确的是（ ）| A． | 物体在A点的机械能为$\frac{1}{2}$mv2+mgh | B． | 物体在A点的机械能为$\frac{1}{2}$mv2+mgH | ||
| C． | 物体在A点的动能为$\frac{1}{2}$mv2+mgH-mgh | D． | 物体在A点的动能为$\frac{1}{2}$mv2+mgh |
20．如图所示，一个环绕中心线AB以一定的加速度转动，下列说法正确的是（ ）
| A． | P、Q两点的加速度相同 | B． | P、Q两点的线速度相同 | ||
| C． | P、Q两点的加速度之比为$\sqrt{3}$：1 | D． | P、Q两点的线速度之比为$\sqrt{3}$：1 |