题目内容
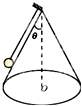
长为l的细线上端固定在顶角为74°的固定光滑圆锥体的顶部,下端与质量为m的小球(可看做质点)相连,如图.让小球绕圆锥体的中心以角速度ω在水平面内做匀速圆周运动.(已知sin37°=0.6;cos37°=0.8)
(1)当ω2=______时,圆锥体对小球的支持力恰好为0;
(2)当ω2=
时,绳对小球的拉力是______;
(3)当ω2=
时,绳对小球的拉力是______.
(1)当ω2=______时,圆锥体对小球的支持力恰好为0;
(2)当ω2=
| ||
| l |
(3)当ω2=
| 5g |
| 9l |

(1)小球刚要离开锥面时的速度,此时支持力为零,根据牛顿第二定律得:
mgtanθ=mω02lsinθ
解得:ω02=
,
(2)当ω2=
>
时,小球离开锥面,设细线与竖直方向夹角为β
T3sinβ=mω2lsinβ
故T3=mlω2=ml?
=
mg
(3)当ω2=
<
时,根据牛顿第二定律得:
Tsinθ-Ncosθ=mω2lsinθ
Tcosθ+Nsinθ=mg
解得:T=mgcosθ+mlω2sin2θ=mg
故答案为:(1)
;(2)
mg;(3)mg
mgtanθ=mω02lsinθ
解得:ω02=
| 5g |
| 4l |
(2)当ω2=
| ||
| l |
| 5g |
| 4l |
T3sinβ=mω2lsinβ
故T3=mlω2=ml?
| ||
| l |
| 2 |
(3)当ω2=
| 5g |
| 9l |
| 5g |
| 4l |
Tsinθ-Ncosθ=mω2lsinθ
Tcosθ+Nsinθ=mg
解得:T=mgcosθ+mlω2sin2θ=mg
故答案为:(1)
| 5g |
| 4l |
| 2 |

练习册系列答案
相关题目



