Question

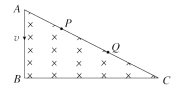
【题目】如图所示， 直角三角形 COD 由粗糙程度不同的材料 A、 B 拼接而成， ∠ODC=37° ，P 为两材料在 CD 边上的交点， 且 CP=PD。 现 OD 边水平放置， 让小物块无初速从 C 点释放， 滑到 D 点时速度刚好为零。 已知小物块与材料 A 在 CP 段的动摩擦因素μ1= 0.6。（ g 取 10 m/s2， sin 37° ＝0.6， cos 37° ＝0.8） 求：

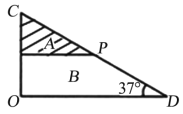
(1).小物块与材料 B 在 PD 段的动摩擦因素μ2；

(2).若将 OC 边水平放置， 再让小物块无初速从 D 点释放， 小物块滑到底端时速率v=7m/s， 则 CD 段的长度为多少？

Answer 1

【答案】（1） （2）

【解析】

（1）设小物块在P点的速度vP，在CP段的加速度为a1，PD段的加速度为a2，，则有：

a1=a2

又a1=gsin37°-μ1gcos37°

a2=μ2gcos37°-gsin37°

解得μ2=0.9

（2）从D到C由动能定理：(设CP=PD=L)

解得L=3.5m，

则CD=2L=7m