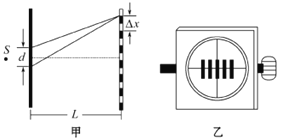
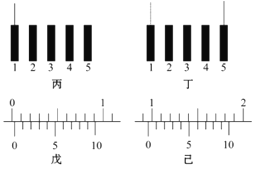
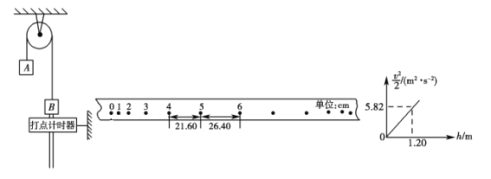
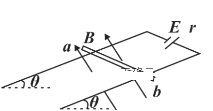
题目内容
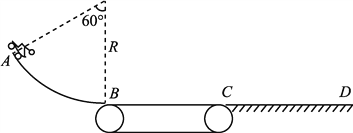
【题目】如图所示为固定在竖直平面内的光滑轨道ABCD,其中ABC部分是半径为R的半圆形轨道(AC是圆的直径),CD部分是水平轨道。一个质量为m的小球沿水平方向进入轨道,通过最高点A时速度大小vA=2![]() ,之后离开A点,最终落在水平轨道上。小球运动过程中所受空气阻力忽略不计,重力加速度为g。求:
,之后离开A点,最终落在水平轨道上。小球运动过程中所受空气阻力忽略不计,重力加速度为g。求:
(1)小球落地点与C点间的水平距离;
(2)小球落地时的速度大小和方向;
(3)小球在A点时轨道对小球的压力的大小。

【答案】(1)4R;(2)![]() ,速度方向与水平方向的夹角为45°;(3)3mg
,速度方向与水平方向的夹角为45°;(3)3mg
【解析】
(1)小球离开A点后做平抛运动根据平抛运动规律,在竖直方向有
2R=![]() gt2
gt2
解得小球运动时间
t=2![]()
在水平方向上有
x=vAt
解得小球落地点与C点间的水平距离
x=4R
(2)设小球落地时的速度方向与水平方向的夹角为θ,则有
tanθ=![]()
解得
θ=45°
即与水平方向的夹角为45°
落地时的速度
![]()
代入数据解得
![]()
(3)设小球在A点时轨道对小球的压力为FN,根据牛顿第二定律
FN+mg=m![]()
解得
FN=3mg

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目