题目内容
14.拱桥结构是古代人们解决建筑跨度的有效方法,像欧洲古罗马的万神庙、我国古代的赵州桥都是拱桥结构的典型建筑.拱桥结构的特点是利用石块的楔形结构,将受到的重力和压力分解为向两边的压力,最后由拱券两端的基石来承受(如图甲).现有六块大小、形状、质量都相等的楔块组成一个半圆形实验拱桥,如图乙所示,如果每个楔块质量m=3kg,则:
(1)六块楔块组成的拱桥对一边支撑物的压力是多大?
(2)如果在中间两个楔块上加一个向下的50N的压力F,那么其两边相邻的支撑物给予楔块的弹力F1与F2分别是多大?(g取9.8N/kg)
分析 (1)对六块楔块组成的整体受力分析,受重力和两侧的支持力,根据平衡条件列式求解即可;
(2)对中间两楔块受力分析,受重力、两个支持力和向下的压力,根据平衡条件列式分析即可
解答 解:(1)对六块楔块组成的整体,根据平衡条件,有:
6mg=2N
解得:
N=3mg=3×3×9.8=88.2N
根据牛顿第三定律,拱券对一边支撑物的压力是88.2N;
(2)以中间两楔块为研究对象,其受力如图所示: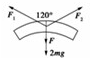
由对称性可知F1=F2
由互成120°的二力合成特点知:
F1=F2=2mg+F=2×3×9.8+50=108.8N
答:(1)六块楔块组成的拱券对一边支撑物的压力是88.2N;
(2)如果在中间两个楔块上加一个向下的50N的压力F,那么其两边相邻的支撑物给予楔块的弹力F1与F2都是108.8N.
点评 本题关键灵活地选择研究对象,受力分析后根据平衡条件列式求解,注意整体法的运用,基础题目.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
5.“嫦娥二号”进入环月轨道后,分别在距月球表面最远100km,最近15km高度的轨道上做圆周运动,此高度远小于月球的半径,设“嫦娥二号”绕月与月绕地的转动方向同向.已知地球的质量为月球质量的k倍,月球绕地球运行的轨道半径为月球的半径的n倍,月球绕地球运行的周期为T.若某时刻“嫦娥二号”距地球最远,经△t时间“嫦娥二号”距地球最近,则△t不可能为( )
| A. | $\frac{T}{2(1-\sqrt{\frac{k}{{n}^{3}}})}$ | B. | $\frac{T}{2(\sqrt{\frac{{n}^{3}}{k}}-1)}$ | C. | $\frac{T}{2(\sqrt{\frac{k}{{n}^{3}}}-1)}$ | D. | $\frac{T}{2(1-\sqrt{\frac{{n}^{3}}{k}})}$ |
9. 农民工是活跃在城镇和乡村中最积极、最能干、最可敬的新生力量.在建筑工地上,他们设计了一种简易的滑轨,将一些建筑材料由高处送到低处,如图所示,两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( )
农民工是活跃在城镇和乡村中最积极、最能干、最可敬的新生力量.在建筑工地上,他们设计了一种简易的滑轨,将一些建筑材料由高处送到低处,如图所示,两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( )
 农民工是活跃在城镇和乡村中最积极、最能干、最可敬的新生力量.在建筑工地上,他们设计了一种简易的滑轨,将一些建筑材料由高处送到低处,如图所示,两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( )
农民工是活跃在城镇和乡村中最积极、最能干、最可敬的新生力量.在建筑工地上,他们设计了一种简易的滑轨,将一些建筑材料由高处送到低处,如图所示,两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( )| A. | 减少每次运送瓦的块数 | |
| B. | 减少两杆之间的距离 | |
| C. | 用比原来较长的两根圆柱形木杆替代原来的木杆 | |
| D. | 用比原来较短的两根圆柱形木杆替代原来的木杆 |
19. 三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
 三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )| A. | 落在a点的颗粒带正电、C点的带负电、b点的不带电 | |
| B. | 落在a、b、c点颗粒在电场中的加速度大小的关系是a>b>c | |
| C. | 三个颗粒在电场中的运动时间关系是a>b>c | |
| D. | 电场力对落在b点的颗粒不做功 |
4.在研究下述运动时,能把物体看作质点的是( )
| A. | 研究地球的自转效应 | |
| B. | 研究乒乓球的旋转效应 | |
| C. | 选万吨货轮为研究对象,确定它在航行过程中某时刻的位置 | |
| D. | 研究一列火车通过长江大桥所需的时间 |
 如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取g=10m/s2,sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取g=10m/s2,sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求: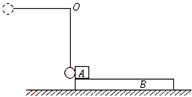 质量为mB=6kg的木板B静止于光滑水平面上,物块A质量为mA=1kg,停在B的左端.质量为m=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞,碰撞时间极短,且无机械能损失.物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.1,A离开B时的速度是B的2倍,g取10m/s2.求木板的长度d?
质量为mB=6kg的木板B静止于光滑水平面上,物块A质量为mA=1kg,停在B的左端.质量为m=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞,碰撞时间极短,且无机械能损失.物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.1,A离开B时的速度是B的2倍,g取10m/s2.求木板的长度d? 如图所示,在竖直平面内建立xOy直角坐标系,Oy表示竖直向上的方向.已知该平面内存在沿x轴负方向的区域足够大的匀强电场,现有一个质量为m=0.05kg,带电量为q=-2.5×10-4C 的小球从坐标原点O沿y轴正方向以一定的初速度竖直向上抛出,它到达的最高点位置为图中的Q点,不计空气阻力,g取10m/s2.
如图所示,在竖直平面内建立xOy直角坐标系,Oy表示竖直向上的方向.已知该平面内存在沿x轴负方向的区域足够大的匀强电场,现有一个质量为m=0.05kg,带电量为q=-2.5×10-4C 的小球从坐标原点O沿y轴正方向以一定的初速度竖直向上抛出,它到达的最高点位置为图中的Q点,不计空气阻力,g取10m/s2.