��Ŀ����
17�� ���Ϊ�ȵ�б����ֻ��AB�δֲڣ���Ħ������Ϊ��=2tan�ȣ����ಿ�ֹ⻬��AB�γ�Ϊ2L����N����ͬ��Сľ�飨��������ÿ��Сľ��ʱ����Ϊ�ʵ㣩��б�濿��һ�𣬵���ճ�ӣ��ܳ�ΪL��ÿһ��Сľ���������Ϊm���������ɾ�ֹ�ͷţ��ͷ�ʱ�¶˾�AΪ2L��B��б����㹻������
���Ϊ�ȵ�б����ֻ��AB�δֲڣ���Ħ������Ϊ��=2tan�ȣ����ಿ�ֹ⻬��AB�γ�Ϊ2L����N����ͬ��Сľ�飨��������ÿ��Сľ��ʱ����Ϊ�ʵ㣩��б�濿��һ�𣬵���ճ�ӣ��ܳ�ΪL��ÿһ��Сľ���������Ϊm���������ɾ�ֹ�ͷţ��ͷ�ʱ�¶˾�AΪ2L��B��б����㹻��������1���ӵ�1��ľ�鵽��N��ľ��ͨ��A��Ĺ����У��ڼ���ľ��ͨ��A����ٶ��������ٶ�Ϊ���٣�
��2��ľ����б���ϻ����Ĺ����У���k-1��ľ��͵�k+1��ľ��Ե�k��ľ�������ܹ���
��3����k��ľ��ͨ��B����ٶȣ�������1��k��N��
���� ��1������n��ľ���A���ٶ����vm�����nmgcos��=Nmgsin�ȣ����n��N�Ĺ�ϵ�����ݶ��ܶ��������������ٶȣ�
��2��ȫ��ľ��չ�A��ʱ�ٶ�Ϊv�����ݶ��ܶ����������v����ľ����б���ϻ���ʱ��ֻ����ͨ��A��Ĺ����вſ��������������������ΪW���Դӿ�ʼ������ľ���ͨ��A��Ĺ��̣����ö��ܶ����������W��
��3��������ľ��չ�A�㵽��k��ľ��յ�B�㣬�Ե�k��ľ�����ö��ܶ���������⣮
��� �⣺ľ���A���λ��Ϊxʱ��Ħ����Ϊ��f=��$\frac{N}{L}$mgcos�ȣ�
Ħ����������λ�ƣ�����ƽ������Ħ����������
��1������n��ľ���A���ٶ����vm�����У���nmgcos��=Nmgsin��
��ã�n=$\frac{N}{2}$����һ��ľ���A���ٶ�����ɶ��ܶ����ã�
$\frac{1}{2}$Nmv2=Nmg•$\frac{5}{2}$Lsin��$\frac{1}{2}$•$\frac{1}{2}$��Nmgcos��•$\frac{L}{2}$��
��ã�vm=$\sqrt{4.5Lgsin��}$��
��2��ȫ��ľ��չ�A��ʱ�ٶ�Ϊv�����У�
Nmgsin��•L-$\frac{1}{2}$��Nmggcos��•L=$\frac{1}{2}$Nmv2-0��
��ã�v=$\sqrt{4Lgsin��}$��
��ľ����б���ϻ���ʱ��ֻ����ͨ��A��Ĺ����вſ��������������
������ΪW���Դӿ�ʼ������ľ���ͨ��A��Ĺ��̣��Ե�k��ľ���У�
mg•3Lsin��-��mgcos�ȣ�N-K��$\frac{L}{N}$+W=mv2-0��
��ã�W=$\frac{N-2K}{N}$mgLsin�ȣ�
��3��������ľ��չ�A�㵽��k��ľ��յ�B�㣬�Ե�k��ľ�飬
�ɶ��ܶ����ã�$\frac{1}{2}$mvB2-$\frac{1}{2}$mv2=��mgsin��-��mgcos�ȣ���k$\frac{L}{N}$+L����
��ã�vB=$\sqrt{\frac{2��N-K��Lsin��}{N}}$��
�𣺣�1���ӵ�1��ľ�鵽��N��ľ��ͨ��A��Ĺ����У���$\frac{N}{2}$��ľ��ͨ��A����ٶ��������ٶ�Ϊ��$\sqrt{4.5Lgsin��}$��
��2��ľ����б���ϻ����Ĺ����У���k-1��ľ��͵�k+1��ľ��Ե�k��ľ�������ܹ�Ϊ$\frac{N-2K}{N}$mgLsin�ȣ�
��3����k��ľ��ͨ��B����ٶ�Ϊ$\sqrt{\frac{2��N-K��Lsin��}{N}}$��
���� ������Ҫ�����˶��ܶ�����ֱ��Ӧ�ã�Ҫ��ͬѧ����ѡȡ���ʵĹ������ö��ܶ�����⣬�Ѷ����У�


��1��ʵ����Ҫ�������£�
�ٽ������������̶���С���ϣ�
��ƽ��Ħ��������С����û����������ʱ��������ֱ���˶���
�۰�ϸ�ߵ�һ�˹̶��������������ϣ���һ��ͨ���������빳��������
�ܽ�ͨ��Դ����C���ͷ�С����С����ϸ���������˶�����¼ϸ������F�Ĵ�С��С���ֱ�A��Bʱ������vA��vB
�ݸı����ҹ�����������ظ��ܵIJ�����
��2�����м�¼��ʵ���õļ������ݣ�vB2-vA2�������ٶȴ�������¼���ʵ�ƽ�������ٶȵı���ʽa=$\frac{{{v}_{B}^{2}-v}_{A}^{2}}{2L}$����������֪�ķ��ű�ʾ�����뽫���е�3�ε�ʵ��������д���������������λ��Ч���֣���
| ���� | F��N�� | vB2-vA2��m2/s2�� | a��m/s2�� |
| 1 | 0.60 | 0.77 | 0.80 |
| 2 | 1.04 | 1.61 | 1.68 |
| 3 | 1.42 | 2.34 | |
| 4 | 2.62 | 4.65 | 4.84 |
| 5 | 3.00 | 5.49 | 5.72 |
| A�� | $\frac{T}{2��1-\sqrt{\frac{k}{{n}^{3}}}��}$ | B�� | $\frac{T}{2��\sqrt{\frac{{n}^{3}}{k}}-1��}$ | C�� | $\frac{T}{2��\sqrt{\frac{k}{{n}^{3}}}-1��}$ | D�� | $\frac{T}{2��1-\sqrt{\frac{{n}^{3}}{k}}��}$ |
 ũ���ǻ�Ծ�ڳ�������������������ܸɡ���ɾ��������������ڽ��������ϣ����������һ�ּ��Ļ��죬��һЩ���������ɸߴ��͵��ʹ�����ͼ��ʾ������Բ����ľ��AB��CD�ƽ�У�б������ֱǽ���ϣ���һ���߷�����ľ�˹��ɵĻ����ϣ��߽��ػ��컬���ʹ�����ʵ�ʲ����з���������ʱ�ٶȽϴ��п���ˤ�飬Ϊ�˷�ֹ�߱������д�ʩ�п��е��ǣ�������
ũ���ǻ�Ծ�ڳ�������������������ܸɡ���ɾ��������������ڽ��������ϣ����������һ�ּ��Ļ��죬��һЩ���������ɸߴ��͵��ʹ�����ͼ��ʾ������Բ����ľ��AB��CD�ƽ�У�б������ֱǽ���ϣ���һ���߷�����ľ�˹��ɵĻ����ϣ��߽��ػ��컬���ʹ�����ʵ�ʲ����з���������ʱ�ٶȽϴ��п���ˤ�飬Ϊ�˷�ֹ�߱������д�ʩ�п��е��ǣ�������| A�� | ����ÿ�������ߵĿ��� | |
| B�� | ��������֮��ľ��� | |
| C�� | �ñ�ԭ���ϳ�������Բ����ľ�����ԭ����ľ�� | |
| D�� | �ñ�ԭ���϶̵�����Բ����ľ�����ԭ����ľ�� |
 A��B����������������������糡�ĵ糡�ߣ�����δ�������ͼ��ʾ��ͼ��C��Ϊ���������ߵ��е㣬MNΪ���������ߵ��д��ߣ�DΪ�д����ϵ�һ�㣬�糡�ߵķֲ�����MN���ҶԳƣ�������˵������ȷ���ǣ�������
A��B����������������������糡�ĵ糡�ߣ�����δ�������ͼ��ʾ��ͼ��C��Ϊ���������ߵ��е㣬MNΪ���������ߵ��д��ߣ�DΪ�д����ϵ�һ�㣬�糡�ߵķֲ�����MN���ҶԳƣ�������˵������ȷ���ǣ�������| A�� | ����������һ���ǵ������ֵ�� | B�� | C��ĵ���һ��С��D��ĵ��� | ||
| C�� | C��ĵ���һ������D��ĵ��� | D�� | C��ĵ糡ǿ�ȱ�D��ĵ糡ǿ��С |
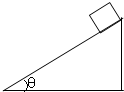 �����Ϊ�ȳ�б���ϣ���һ�����з緫�Ļ���Ӿ�ֹ��ʼ��б���»�����������Ϊm������б���Ļ���Ħ������Ϊ�̣��緫�ܵ��Ŀ��������뻬���»����ٶȴ�С�����ȣ���f=kv����
�����Ϊ�ȳ�б���ϣ���һ�����з緫�Ļ���Ӿ�ֹ��ʼ��б���»�����������Ϊm������б���Ļ���Ħ������Ϊ�̣��緫�ܵ��Ŀ��������뻬���»����ٶȴ�С�����ȣ���f=kv����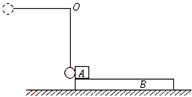 ����ΪmB=6kg��ľ��B��ֹ�ڹ⻬ˮƽ���ϣ����A����ΪmA=1kg��ͣ��B����ˣ�����Ϊm=1kg��С���ó�Ϊl=0.8m�����������ڹ̶���O�ϣ���������ֱ��ˮƽλ�ú��ɾ�ֹ�ͷ�С��С������͵���A������ײ����ײʱ�伫�̣�����е����ʧ�������С�����Ϊ�ʵ㣬���ƿ�����������֪A��B��Ķ�Ħ��������=0.1��A�뿪Bʱ���ٶ���B��2����gȡ10m/s2����ľ��ij���d��
����ΪmB=6kg��ľ��B��ֹ�ڹ⻬ˮƽ���ϣ����A����ΪmA=1kg��ͣ��B����ˣ�����Ϊm=1kg��С���ó�Ϊl=0.8m�����������ڹ̶���O�ϣ���������ֱ��ˮƽλ�ú��ɾ�ֹ�ͷ�С��С������͵���A������ײ����ײʱ�伫�̣�����е����ʧ�������С�����Ϊ�ʵ㣬���ƿ�����������֪A��B��Ķ�Ħ��������=0.1��A�뿪Bʱ���ٶ���B��2����gȡ10m/s2����ľ��ij���d��