题目内容
2.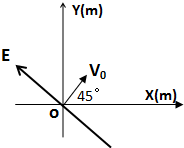 如图所示,在水平光滑绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c.某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,V0与水平匀强电场垂直,
如图所示,在水平光滑绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c.某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,V0与水平匀强电场垂直,(1)该带电小球所受到的电场力的大小;
(2)该带电小球在第二秒内的速度变化量;
(3)当带电小球再经过X轴时与X轴交于A点,求带电小球经过A点时速度V=?经历的时间t=?OA两点之间的电势差UOA=?
分析 (1)直接由公式F=qE求出电场力;
(2)根据牛顿第二定律求出加速度,再求出速度的变化;
(3)由位移公式,依据运动的合成与分解,从而求出坐标;由U=Ed,可求出电势差.
解答 解:(1)带电粒子受到的电场力:F=qE=2×10-6×103N=2×10-3N
(2)由牛顿第二定律得:a=$\frac{F}{m}$=$\frac{2×1{0}^{-3}}{1×1{0}^{-3}}m/{s}^{2}=2m/{s}^{2}$,
速度的变化量△v=at,
代入数据解得△v=2m/s.
(3)建垂直初速度方向为y轴,沿初速度方向为x轴,因为tan45°=$\frac{\frac{{v}_{y}}{2}t}{{v}_{0}t}$,解得vy=2v0=4m/s.
则A点的速度v=$\sqrt{{{v}_{y}}^{2}+{{v}_{0}}^{2}}=\sqrt{16+4}=2\sqrt{5}m/s$.
则运动的时间t=$\frac{{v}_{y}}{a}=\frac{4}{2}s=2s$.
OA间的电势差${U}_{OA}=-Ey=-E•\frac{1}{2}a{t}^{2}$=-$1{0}^{3}×\frac{1}{2}×2×4V$=-4×103V.
答:(1)该带电小球所受到的电场力是2×10-3N;
(2)该带电小球在第二秒内速度的变化量是2m/s;
(3)带电小球经过A点时速度V为2$\sqrt{5}$m/s,时间t为2s、OA间电势差UOA=-4×103V.
点评 理解运动合成与分解的方法,并运用三角函数关系来综合求解,最后还注意U=Ed式中的d的含义.

练习册系列答案
相关题目
12.在地球表面不同纬度的物体,因随地球自转而做匀速圆周运动,下列说法中正确的是( )
| A. | 这些物体运动的角速度相同 | B. | 这些物体运动的线速度相同 | ||
| C. | 这些物体运动向心加速度相同 | D. | 这些物体运动的线速度大小相等 |
10.下列几种运动中一定是自由落体运动的是( )
| A. | 物体仅仅在重力作用下的运动 | |
| B. | 物体只受重力而且由静止开始的运动 | |
| C. | 物体以重力加速度所做的初速为0的匀加速运动 | |
| D. | 满足前n s内位移之比为s1:s2:s3:…:sn=12:22:32:…:n2的运动 |
7. 如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
 如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )| A. | 该图线的斜率为$\frac{h}{e}$(h为普朗克常量,e为元电荷量) | |
| B. | 该金属的逸出功为0.5 eV | |
| C. | 该金属的截止频率为5.5×1014Hz | |
| D. | 该金属的截止频率为4.27×1014Hz |
14.对于一块普通指针钟表,则( )
| A. | 分针的转动周期为1小时 | |
| B. | 时针的转动周期为24小时 | |
| C. | 若分针的长度是时针的2倍,分针端点的线速度分针是时针的24倍 | |
| D. | 若分针的长度是时针的2倍,分针端点的线速度分针是时针的48倍 |
11.组成星球的物质是靠万有引力吸引在一起的,这样的星球有一个最大的自转速率,如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做圆周运动,由此能得到半径为R、质量为M且均匀分布的星球的最小自转周期T,下列表达式中正确的是( )
| A. | T=2π$\sqrt{\frac{R^3}{GM}}$ | B. | T=2π$\sqrt{\frac{{2{R^3}}}{GM}}$ | C. | T=2π$\sqrt{\frac{{3{R^3}}}{GM}}$ | D. | T=π$\sqrt{\frac{R^3}{GM}}$ |
12.关于生活中的实际情形,下列说法正确的是( )
| A. | 电容器外壳上标的电压是额定电压,这个数值比击穿电压低 | |
| B. | 汽车在通过水库泄洪闸下游的凹形桥的最低点时,驾驶员处于失重状态 | |
| C. | 为了便于行车,高大的桥通常要造很长的引桥,以减小汽车重力垂直桥面的分力 | |
| D. | 电动机等大功率设备内部含有多匝线圈,在开关断开时,因线圈自感产生电火花 |
 如图,一长木板位于光滑水平面上,长木板的左端固定一挡板,木板和挡板的总质量为M=3.0kg,木板的长度为L=1.5m.在木板右端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速度v0沿木板向左滑动,重力加速度g取10m/s2.
如图,一长木板位于光滑水平面上,长木板的左端固定一挡板,木板和挡板的总质量为M=3.0kg,木板的长度为L=1.5m.在木板右端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速度v0沿木板向左滑动,重力加速度g取10m/s2.