题目内容
7. 如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )| A. | 该图线的斜率为$\frac{h}{e}$(h为普朗克常量,e为元电荷量) | |
| B. | 该金属的逸出功为0.5 eV | |
| C. | 该金属的截止频率为5.5×1014Hz | |
| D. | 该金属的截止频率为4.27×1014Hz |
分析 根据爱因斯坦光电效应方程Ek=hγ-W,Ek-γ图象的斜率等于h.横轴的截距大小等于截止频率,逸出功W=hγ0,根据数学知识进行求解.
解答 解:A、由Ek=hγ-W,得知,该图线的斜率表示普朗克常量h.故A错误.
B、当Ek=hγ-W=0时,逸出功为W=hγ0=$\frac{0.5×1.6×1{0}^{-19}}{(5.5-4.27)×1{0}^{14}}$×4.27×1014 Hz=2.7755×10-19J≈1.73eV,B错误;
CD、根据爱因斯坦光电效应方程Ek=hγ-W,Ek-γ图象的横轴的截距大小等于截止频率,由图知该金属的截止频率为4.27×1014 Hz,故C错误,D正确.
故选:D.
点评 解决本题的关键掌握光电效应方程,以及知道逸出功与极限频率的关系,结合数学知识即可进行求解.

练习册系列答案
相关题目
18.关于物体的内能,下列说法正确的是( )
| A. | 热水的内能一定比冷水的大 | |
| B. | 当温度等于0℃时,分子动能为零 | |
| C. | 分子间距离为r0时,分子势能为零 | |
| D. | 温度相等的氢气和氧气,它们的分子平均动能相等 |
15. 在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
计算小车通过计数点“2”的瞬时速度公式为v2=$\frac{{{d_2}-{d_1}}}{2T}$(以d1、d2及相邻计数点间时间T来表示)代入得v2=0.21m/s.(结果保留两位有效数字)
 在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.| 距离 | d1 | d2 | d3 |
| 测量值/cm | 1.20 | 5.40 | 12.02 |
12.下列说法正确的是( )
| A. | 开普勒通过观察天象以及深入研究第谷的数据提出行星运动三大定律 | |
| B. | 相对论和量子力学的出现,使经典力学失去了意义 | |
| C. | 第三宇宙速度达到16.7 km/s,已经超出了经典力学的使用范围 | |
| D. | 牛顿是经典力学的奠基人,他提出了牛顿运动定律与万有引力定律 |
19.“神舟七号”飞船的成功着陆,标志着我国成为世界上第三个独立掌握载人航天技术并能够进行太空行走的国家.为了保证航天员的安全,飞船上使用了降落伞、反推火箭、缓冲座椅三大法宝,在距离地面大约1m时,返回舱的4个反推火箭点火工作,返回舱速度一下子降到了2m/s以内,随后又渐渐降到1m/s,最终安全着陆.把返回舱离地1m开始到完全着陆称为着地过程,则关于反推火箭的作用,下列说法正确的是( )
| A. | 减小着地过程中返回舱和航天员的动量变化 | |
| B. | 减小着地过程中返回舱和航天员所受的冲量 | |
| C. | 延长着地过程的作用时间 | |
| D. | 减小着地过程返回舱和航天员所受的平均冲力 |
16. 用如图电路研究光电效应规律.其中标有A和K的为光电管,K为阴极,当受光照射时可产生光电效应现象,A为阳极.理想电流计G可检测通过光电管的电流,理想电压表用来测量光电管两端电压.现接通电源,用光子能量为l0.5eV的光照射阴极,电流计中有示数,当滑动变阻器滑片P缓慢向右滑动时,电流计示数逐渐减小,当滑至某一位置时电流计示数恰好为0,读出此时电压表的示数为6.0V;现保持滑片P的位置不动,改用光子能量为12eV的光照射阴极,则( )
用如图电路研究光电效应规律.其中标有A和K的为光电管,K为阴极,当受光照射时可产生光电效应现象,A为阳极.理想电流计G可检测通过光电管的电流,理想电压表用来测量光电管两端电压.现接通电源,用光子能量为l0.5eV的光照射阴极,电流计中有示数,当滑动变阻器滑片P缓慢向右滑动时,电流计示数逐渐减小,当滑至某一位置时电流计示数恰好为0,读出此时电压表的示数为6.0V;现保持滑片P的位置不动,改用光子能量为12eV的光照射阴极,则( )
 用如图电路研究光电效应规律.其中标有A和K的为光电管,K为阴极,当受光照射时可产生光电效应现象,A为阳极.理想电流计G可检测通过光电管的电流,理想电压表用来测量光电管两端电压.现接通电源,用光子能量为l0.5eV的光照射阴极,电流计中有示数,当滑动变阻器滑片P缓慢向右滑动时,电流计示数逐渐减小,当滑至某一位置时电流计示数恰好为0,读出此时电压表的示数为6.0V;现保持滑片P的位置不动,改用光子能量为12eV的光照射阴极,则( )
用如图电路研究光电效应规律.其中标有A和K的为光电管,K为阴极,当受光照射时可产生光电效应现象,A为阳极.理想电流计G可检测通过光电管的电流,理想电压表用来测量光电管两端电压.现接通电源,用光子能量为l0.5eV的光照射阴极,电流计中有示数,当滑动变阻器滑片P缓慢向右滑动时,电流计示数逐渐减小,当滑至某一位置时电流计示数恰好为0,读出此时电压表的示数为6.0V;现保持滑片P的位置不动,改用光子能量为12eV的光照射阴极,则( )| A. | 光电管阴极材料的逸出功为4.5eV | |
| B. | 电流计示数仍然为0 | |
| C. | 光电子的最大初动能一定变大 | |
| D. | 若换用光子能量为9.5eV的光照射阴极,同时将滑片P向左移动少许,电流计示数一定不为0 |
 细线一端拴一个小球,另一端固定.设法使小球在水平面内做匀速圆周运动,如图所示.细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求:
细线一端拴一个小球,另一端固定.设法使小球在水平面内做匀速圆周运动,如图所示.细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求: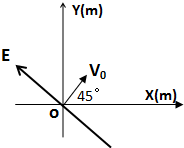 如图所示,在水平光滑绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c.某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,V0与水平匀强电场垂直,
如图所示,在水平光滑绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c.某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,V0与水平匀强电场垂直,