题目内容
如图所示，半径为R、圆心为O的大圆环固定在竖直平面内，两个轻质小圆环套在大圆环上．一根轻质长绳穿过两个小圆环，它的两端都系上质量为m的重物，忽略小圆环的大小，小圆环可以在大圆环上自由移动，且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略，问两个小圆环分别在此位置时，系统可处于平衡状态，求解θ
分析：对小圆环受力分析，抓住小圆环所受的拉力相等，根据它受力分析，求出θ的大小．
解答：解：设平衡时，两小圆环在大圆环竖直对称轴两侧α角的位置上，对于重物m，受绳子拉力T与重力mg作用，有T=mg．
对于小圆环，受到三个力的作用，水平绳子的拉力T、竖直绳子的拉力T、大圆环的支持力N．两绳子的拉力沿大圆环切向的分力大小相等，方向相反Tsinθ=Tsinθ’得θ=θ’，而θ+θ′=90°，所以θ=45°．
答：系统可处于平衡状态θ=45°．
对于小圆环，受到三个力的作用，水平绳子的拉力T、竖直绳子的拉力T、大圆环的支持力N．两绳子的拉力沿大圆环切向的分力大小相等，方向相反Tsinθ=Tsinθ’得θ=θ’，而θ+θ′=90°，所以θ=45°．
答：系统可处于平衡状态θ=45°．
点评：解决本题的关键能够正确地进行受力分析，运用共点力平衡进行求解．
练习册系列答案
相关题目
（2006?淮北模拟）如图所示，半径为R，内径很小的光滑半圆管竖直放置．两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75mg，求a、b两球落地点间的距离．
如图所示，半径为R 的光滑圆形轨道竖直固定放置，质量为m 的小球在圆形轨道内侧做圆周运动．小球通过轨道最高点时恰好与轨道间没有相互作用力．已知当地的重力加速度大小为g，不计空气阻力．试求：
如图所示，半径为R的圆筒绕竖直中心轴OO′转动，小物块A靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ（认为最大静摩擦力等于滑动摩擦力），现要使A不下落，则圆筒转动的角速度ω至少为（ ）
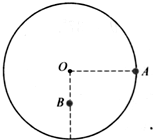如图所示，半径为R，质量不计的圆盘盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平固定轴O，在盘的最右边缘处固定一个质量为m的小球A，在O点的正下方离O点R/2处固定一个质量也为m的小球B，放开盘让其自由转动，问：