题目内容
4.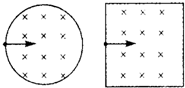 两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )
两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )| A. | 两电子在磁场中运动的时间有可能相同 | |
| B. | 两电子在两磁场中运动时,其半径可能不相同 | |
| C. | 进入圆形磁场区域的电子可能先飞离磁场 | |
| D. | 进入圆形磁场区域的电子可能后飞离磁场 |
分析 电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,通过qvB=m$\frac{{v}^{2}}{r}$得到半径的表达式,判断半径是否相同;运动时间的判断可以根据粒子转过的圆心角的大小;比较哪个磁场电子先出磁场,可以作出多个轨迹比较即可.
解答 解:A、电子在磁场中的可能运动情况如图所示,电子从O点水平进入,由于它们进入圆形磁场和正方形磁场的轨道半径、速度是相同的,把圆形磁场和矩形磁场的边界放到同一位置如图所示,由图可以看出进入磁场区域的电子的轨迹1,先出圆形磁场,再出正方形磁场;进入磁场区域的电子的轨迹2,同时从圆形与正方形边界处磁场;进入磁场区域的电子的轨迹3,先出圆形磁场,再出正方形磁场;所以两电子在磁场中运动的时间有可能相同,电子不会先出正方形的磁场,即进入圆形区域的电子可能先飞离磁场,故A、C正确,D错误.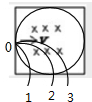
B、根据qvB=$m\frac{{v}^{2}}{r}$得,r=$\frac{mv}{qB}$,速度相同,磁感应强度相同,则粒子运动的轨道半径相等,故B错误.
故选:AC.
点评 本题的难点在于能否想到在同一个图象中做出多个轨迹进行比较哪个先出磁场,根据轨迹对应的圆心角分析电子在磁场中运动的时间,是常用的方法和思路,是熟练掌握.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
14.关于经典力学和相对论、量子力学,下列说法正确的是( )
| A. | 不论是对宏观物体,还是微观粒子,经典力学和量子力学都是适用的 | |
| B. | 经典力学适用于低速运动的物体,相对论适用于高速运动的物体 | |
| C. | 经典力学适用于宏观物体的运动,量子力学适用于微观粒子的运动 | |
| D. | 相对论与量子力学否定了经典力学理论 |
12.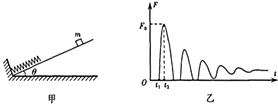 如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
 如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )| A. | 物块运动过程中,物块和弹簧组成的系统机械能守恒 | |
| B. | 物块运动过程中,t1到t2某时刻速度最大 | |
| C. | 物块运动过程中的最大加速度大小为$\frac{{F}_{0}-mgsinθ+μmgcosθ}{m}$ | |
| D. | 最终静止时,物块受到的重力、斜面支持力和摩擦力的合力方向沿斜面向上 |
9.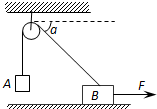 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )| A. | 物体A也做匀速直线运动 | B. | 物体A将竖直向上先加速后减速 | ||
| C. | 物体A将处于超重状态 | D. | 绳子对物体A的拉力保持不变 |
14.一轻杆一端固定质量为m的小球,以另一端为圆心在竖直平面内作圆周运动,轻杆长为l,以下说法中正确的是( )
| A. | 小球过最高点时,杆的弹力可以等于零 | |
| B. | 小球过最高点时的最小速度为$\sqrt{gl}$ | |
| C. | 小球到最高点时速度v>0,小球一定能通过最高点做圆周运动 | |
| D. | 小球过最高点时,杆对球的作用力一定与小球所受重力方向相反 |
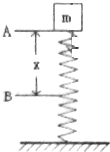 已知弹簧的弹性势能的表达式为Ep=$\frac{1}{2}$kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,现有一轻质弹簧竖直放置在水平面上,如图,今将一质量为m的物块轻放在弹簧上,试求当物块下落到最低点时的加速度.
已知弹簧的弹性势能的表达式为Ep=$\frac{1}{2}$kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,现有一轻质弹簧竖直放置在水平面上,如图,今将一质量为m的物块轻放在弹簧上,试求当物块下落到最低点时的加速度.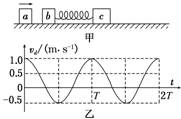 如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则:
如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则: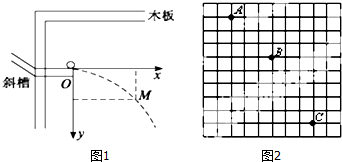 在“研究平抛物体的运动”的实验中:
在“研究平抛物体的运动”的实验中: 用油膜法估测分子的大小,方法及实验步骤如下:
用油膜法估测分子的大小,方法及实验步骤如下: