题目内容
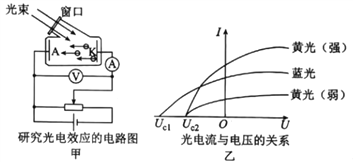
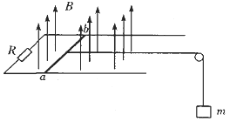
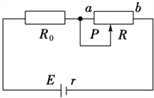
【题目】如图甲所示,斜面上存在一有理想边界的匀强磁场,磁场方向与斜面垂直。在斜面上离磁场上边界0.36m处由静止释放一单匝矩形金属线框,线框底边和磁场边界平行,金属线框与斜面间的动摩擦因数0.5。整个线框进入磁场的过程中,机械能E和位移之间的关系如图乙所示。已知E0-E1=0.09J,线框的质量为0.1kg,电阻为0.06
,斜面倾角370,磁场区域的宽度d=0.43m,求:
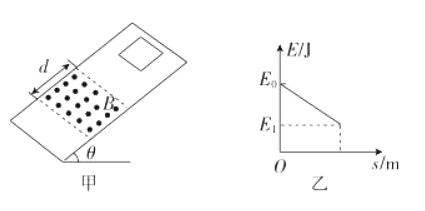
（1）.线框刚进入磁场时的速度大小v1;
（2）.线框从开始进入至完全进入磁场所用的时间t;
（3）.线框穿越磁场的整个过程中电功率的最大值。
【答案】（1）1.2m/s （2）0.125s （3） 0.43W
【解析】试题分析：（1）金属线框进入磁场的过程中，减小的机械能等于克服摩擦力和安培力所做的功，机械能仍均匀减小，因为安培力也为恒力，线框做匀速运动，根据牛顿第二定律和运动学公式求出线框进入磁场时的速度；
（2）结合功能关系求出线框进入磁场时的距离，从而得出金属线框刚进入磁场到恰完全进入磁场所用的时间．
（3）线框刚出磁场时速度最大，线框内的电功率最大，根据速度位移公式求出线框出磁场时的速度，根据线框进入磁场时匀速运动得出安培力的大小，综合功率的表达式求出最大电功率．
解：(1) 金属线框进入磁场的过程中，减小的机械能等于克服摩擦力和安培力所做的功，机械能仍均匀减小，因为安培力也为恒力，线框做匀速运动．则有：
v12=2as1，其中a=gsin37°-μgcos37°=2m/s2
可解得线框刚进入磁场时的速度大小为：v1=1.2m/s；
(2) 设线框边长为s2，即线框进入磁场过程中运动的建立为s2，
根据功能关系可得：△E2=Wf2+WA=（f+FA）s2，
其中有：△E2=（0.756-0.666）J=0.09J，f+FA=mgsin37°=0.6N，s2为线框的侧边长，
解得：s2=0.15m
；
(3) 线框刚出磁场时速度最大，线框内的电功率最大
由v22=v12+2a（d-s2），
解得：v2=1.6m/s
根据线框匀速进入磁场时，有：FA+μmgcos37°=mgsin37°
可求出：FA=0.2N
因为
求得：B2L2=0.01T2m2
将v2、B2L2的值代入得：Pm=I2R=0.43W．
点晴：对于电磁感应问题研究思路常常有两条：一条从力的角度，重点是分析安培力作用下导体棒的平衡问题，根据平衡条件列出方程；另一条是能量，分析涉及电磁感应现象中的能量转化问题，根据动能定理、功能关系等列方程求解．解决本题的关键能通过图象分析出物体的运动状况：先做匀加速，再做匀速，接着做匀加速．以及能对线框进行正确的受力分析和熟练运用运动学公式。
