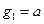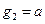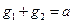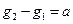题目内容
两行星A和B是两个均匀球体,行星A的卫星a沿圆轨道运行的周期Ta;行星B的卫星b沿圆轨道运行的周期为Tb.设两卫星均为各中心星体的近表卫星,而且Ta:Tb=1:4,行星A和行星B的半径之比RA:RB=1:2,则行星A和行星B的密度之比ρA:ρB=______,行星表面的重力加速度之比gA:gB=______.
人造地球卫星的万有引力充当向心力,即:
G
| Mm |
| R2 |
| 4π2 |
| T2 |
体积为:
V=
| 4πR3 |
| 3 |
解得密度为:
ρ=
| M |
| V |
| 3π |
| GT2 |
故AB密度之比为:
ρA:ρB=12:42=1:16
忽略行星自转的影响,根据万有引力等于重力列出等式:
G
| Mm |
| R2 |
由①③解得:
g=
| 4π2R |
| T2 |
所以两行星表面处重力加速度之比为:
gA:gB=
| 1 |
| 12 |
| 2 |
| 42 |
故答案为:16:1;8:1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

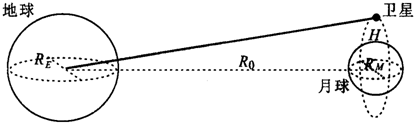
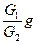
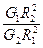
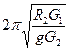
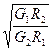
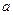 ,设月球表面的重力加速度大小为
,设月球表面的重力加速度大小为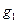 ,在月球绕地球运行的轨道处由地球引力产生的加速度大小为
,在月球绕地球运行的轨道处由地球引力产生的加速度大小为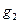 ,则
,则