题目内容
9. 一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关 系,他的实验如下:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小球在空中飞行后落到水平地面,水平距离为S.
一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关 系,他的实验如下:在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小球在空中飞行后落到水平地面,水平距离为S. (1)请你推导出弹簧的弹性势能EP与小钢球质量m、桌面离地面高度h,水平距离S等物理量的关系式:EP=$\frac{mg{s}^{2}}{4h}$.
(2)弹簧的压缩量x与对应的钢球在空中飞行的水平距离S的实验数据如表所示:
| 弹簧长度压缩量x(cm) | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 钢球飞行水平距离S(m) | 1.01 | 1.50 | 2.01 | 2.48 | 3.01 | 3.50 |
分析 根据平抛运动规律可以求出钢球离开桌面时的速度大小,根据功能关系可以求出弹性势能的表达式.
先从实验数据得出弹簧的压缩量与小球的射程的关系,再结合第一小问中结论得到弹性势能与小球的射程的关系,最后综合出弹簧的弹性势能EP与弹簧长度的压缩量x之间的关系.
解答 解:(1)设桌子高度为h,小球离开桌面后做平抛运动,
水平方向:s=v0t,
竖直方向有:h=$\frac{1}{2}g{t}^{2}$
联立解得:v0=$s\sqrt{\frac{g}{2h}}$,
根据功能关系可知弹簧弹性势能转化为小球平抛的初动能,有:
EP=$\frac{1}{2}m{{v}_{0}}^{2}$,解得EP=$\frac{mg{s}^{2}}{4h}$.
(2)Ep与弹簧的压缩量x之间的关系为:Ep与x2成正比.
猜测的理由:由于EP=$\frac{mg{s}^{2}}{4h}$,可知Ep与s2成正比,由表中数据可看出,在误差范围内,x正比于s,猜测可能Ep与x2也成正比.
故答案为:(1)EP=$\frac{mg{s}^{2}}{4h}$,(2)EP与x2 成正比.
点评 本题借助于平抛运动以及数学推导考查了弹性势能和弹性形变量之间的关系,是考查知识综合应用、公式理论推导的好题,其中得到弹性势能表达式是个重点,难点是猜测Ep与弹簧的压缩量x之间的关系,弹性势能的表达式为:${E}_{p}=\frac{1}{2}k{x}^{2}$,故我们的猜测是完全正确的.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
3.在电场和重力场都存在的空间中,一带电小球从A点运动到B点,电场力做了10J的功,重力做了6J的功,克服阻力做了7J的功,则此过程中带电小球的( )
| A. | 机械能增加了10 J,动能减少了7 J | |
| B. | 机械能减少了7 J,动能增加了10 J | |
| C. | 电势能增加了10 J,动能增加了9 J | |
| D. | 电势能减少了10 J,重力势能减少了6J |
4.我国的举重运动,是在世界级大赛中多次摘金夺银的传统体育项目.本届奥运会中我国的举重选手陈艳青、石智勇、张国政、刘春红、唐功红获得雅典奥运会举重冠军.石智勇获得了雅典奥运会男子举重62公斤级冠军,成绩是325公斤.假设杠铃的直径是0.50m,石智勇将杠铃举到离地面2.10m高处,则他在抓举、挺举中总共对杠铃至少做的功为:(g取10m/s2)( )
| A. | 5200J | B. | 6012.5J | C. | 6825J | D. | 3575J |
1. 如图所示,在绝缘光滑水平面上,有一个正方形的abcd,顶点a、c两处分别固定一个正点电荷,电荷量相等.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd做往复运动.粒子从b点运动到d点的过程中( )
如图所示,在绝缘光滑水平面上,有一个正方形的abcd,顶点a、c两处分别固定一个正点电荷,电荷量相等.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd做往复运动.粒子从b点运动到d点的过程中( )
 如图所示,在绝缘光滑水平面上,有一个正方形的abcd,顶点a、c两处分别固定一个正点电荷,电荷量相等.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd做往复运动.粒子从b点运动到d点的过程中( )
如图所示,在绝缘光滑水平面上,有一个正方形的abcd,顶点a、c两处分别固定一个正点电荷,电荷量相等.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd做往复运动.粒子从b点运动到d点的过程中( )| A. | 先做匀加速运动,后做匀减速运动 | |
| B. | 电势先减小后增大 | |
| C. | 电势能与机械能之和先增大,后减小 | |
| D. | 电势能先减小,后增大 |
18. 如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
 如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )| A. | 导体棒运动过程中的最大速度$\frac{mgsinθ}{{{B^2}{l^2}}}$ | |
| B. | R上的最大热功率为$\frac{{m}^{2}{g}^{2}Rsi{n}^{2}θ}{{B}^{2}{L}^{2}}$ | |
| C. | 导体棒返回到ab位置前已经达到下滑的最大速度 | |
| D. | 导体棒返回到ab位置时刚好达到下滑的最大速度 |
19. 如图所示,质量不计的定滑轮用轻绳悬挂在B点,另一条轻绳一端系重物C,绕过滑轮后,另一端固定在墙上A点,若改变B点位置,使滑轮位置发生移动,但使AO段绳子始终保持水平,则可以判断悬点B所受拉力F的大小变化情况是( )
如图所示,质量不计的定滑轮用轻绳悬挂在B点,另一条轻绳一端系重物C,绕过滑轮后,另一端固定在墙上A点,若改变B点位置,使滑轮位置发生移动,但使AO段绳子始终保持水平,则可以判断悬点B所受拉力F的大小变化情况是( )
 如图所示,质量不计的定滑轮用轻绳悬挂在B点,另一条轻绳一端系重物C,绕过滑轮后,另一端固定在墙上A点,若改变B点位置,使滑轮位置发生移动,但使AO段绳子始终保持水平,则可以判断悬点B所受拉力F的大小变化情况是( )
如图所示,质量不计的定滑轮用轻绳悬挂在B点,另一条轻绳一端系重物C,绕过滑轮后,另一端固定在墙上A点,若改变B点位置,使滑轮位置发生移动,但使AO段绳子始终保持水平,则可以判断悬点B所受拉力F的大小变化情况是( )| A. | 若B左移,F将增大 | B. | 若B右移,F将增大 | ||
| C. | 无论B是左移还是右移,F都不变 | D. | 无论B是左移还是右移,F都减小 |
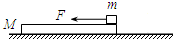 如图所示,质量为M=5kg的木板静止在光滑的水平面上,木板的上端有一质量为m=4kg的木块,以水平向左的恒力F=15N作用于木块上.已知木块与木板间的动摩擦因数μ=0.5,求4s内摩擦力对木板做的功.(最大静摩擦力等于滑动摩擦力).
如图所示,质量为M=5kg的木板静止在光滑的水平面上,木板的上端有一质量为m=4kg的木块,以水平向左的恒力F=15N作用于木块上.已知木块与木板间的动摩擦因数μ=0.5,求4s内摩擦力对木板做的功.(最大静摩擦力等于滑动摩擦力).