Question

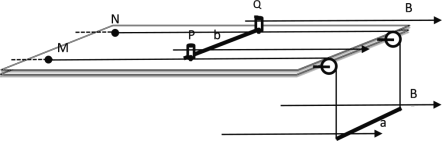
【题目】如图所示，导体棒a两端系有两根足够长的、质量和电阻可忽略的柔软导线，导线通过绝缘水平桌面上的轻质小滑轮，穿过立柱P、Q底部的小孔，固定于桌面上的M、N两点。导体棒b置于立柱P、Q左侧，放置在导线上，与两导线接触良好。两导体棒与桌边缘平行，整个装置处于水平向右、磁感应强度为B的匀强磁场中。已知两根棒的质量均为m，电阻均为R，长度均为L，棒b与导线间的动摩擦因数为μ（μ<1），其余各处均光滑，重力加速度为g。现同时松开M、N两点，棒a由静止开始向下运动。

（1）求棒a向下运动速度为v时，棒b中感应电流的大小及方向；

（2）求棒a向下运动速度为v时，棒b所受安培力大小和摩擦力大小；

（3）求棒a在下落过程中的最大速度vm；

（4）若将桌面以上空间的磁场方向改为水平向左，磁感应强度大小保持不变，桌面以下空间的磁场维持原状，求立柱P、Q对棒b的弹力大小范围。

Answer 1

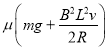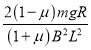【答案】(1) 方向由P指向Q (2) (3) 　(4)

【解析】

(1)当金属棒a以速度v向下运动时，产生感应电动势：

通过b棒的感应电流：

方向由P指向Q 。

(2)金属棒b所受安培力：

金属棒b受力分析如图（a）

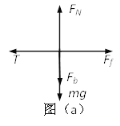
b棒处于平衡状态，由平衡条件得：FN=mg+Fb，

又Ff=μFN

金属棒b所受摩擦力：

Ff＝μFN=μ（mg+）；

(3)金属棒a和两根金属线沿运动方向受力如图（b），Fa为金属棒a所受安培力，Ff＇为b棒对金属线的摩擦力。

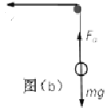
由牛顿第三定律可知：

Ff＇＝Ff＝μ（mg+），

，

a棒向下加速运动，由牛顿第二定律得：

即：

mg--μ（mg+）=ma，

金属棒做加速度逐渐减小的加速运动，当加速度为零时速度达到最大值vm，因此：

mg--μ（mg+）=0，

解得：

；

(4)桌面及其以上空间的匀强磁场，改为水平向左后，b棒受力如图（c），a棒和两根金属线沿运动方向受力如图（d）。

金属棒b：FN1=mg-Fb 、T=Ff1

a棒向下运动时，立柱P、Q对棒的弹力 ：

T =Ff1＝μFN1=μ（mg-），

当开始运动时，弹力T有最大值Tmax趋向于μmg 　

a棒向下加速运动，由牛顿第二定律得：

即：

mg--μ（mg-）=ma，

金属棒a做加速度逐渐减少的加速运动。当加速度为零时速度达到最大值时，弹力T有最小值。即

mg--μ（mg-）=0 ，

解得：

或 μ=1（舍去）

代入得弹力T最小值：Tmin= 0

因此立柱P、Q对金属棒b的弹力大小范围是（0，μmg）。