题目内容
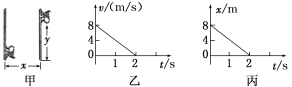
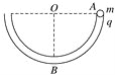
【题目】如图所示,在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷,将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无作用力.若小球所带电荷量很小,不影响O点处的点电荷的电场,则放于圆心O处的点电荷在OB连线的中点处的电场强度大小( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
小球沿细管滑到最低点B过程中,只有重力做功,小球的机械能守恒.小球到达B点时对管壁恰好无压力,则由重力和点电荷对的电场力的合力提供向心力,根据机械能守恒定律求出小球到达B点时的速度,由牛顿第二定律求出场强的大小。
设细管的半径为R,小球到达B点时速度大小为v。小球从A滑到B的过程,由机械能守恒定律得:
![]()
解得:![]()
小球经过B点时,由牛顿第二定律得:
![]()
将![]()
代入得:![]()
根据点电荷的电场强度:![]()
可知,放于圆心O处的点电荷在OB连线的中点处的电场强度大小,![]() ,故D正确,ABC错误。
,故D正确,ABC错误。
故应选:D。

练习册系列答案
相关题目