��Ŀ����
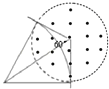
����Ŀ����ͼ��ʾ��һ����������Ϊm=2.0��10��11kg�������q=+1.0��10��5C���Ӿ�ֹ��ʼ����ѹΪU1=100V�ĵ糡���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У�������糡ʱ��ƫת�Ǧ�=60�㣬�������ذ뾶�������һ����ֱֽ�������Բ����ǿ�ų�����������ų�ʱ��ƫת��ҲΪ��=60�㣮��֪ƫת�糡�н����峤L=2cm��Բ����ǿ�ų��İ뾶R=10![]() cm���������Բ��ƣ���
cm���������Բ��ƣ���

��1����������U1=100V�ĵ糡���ٺ�����ʣ�
��2�����������ƫת�糡�ĵ糡ǿ��E��
��3����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�С��
���𰸡���1����������U1=100V�ĵ糡���ٺ������Ϊ1��104m/s��
��2�����������ƫת�糡�ĵ糡ǿ��EΪ10000V/m��
��3����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�СΪ0.13T��
���������⣺��1�������������ٵ糡���ٺ��ٶ�Ϊv1��
���ݶ��ܶ�����qU1=![]() mv12��0 ��
mv12��0 ��
�������ݽ�ã�v1=1��104m/s �ڣ�
��2����������ƫת�糡��ֻ�ܵ糡�����ã�����ƽ���˶���
��ˮƽ������������ֱ���˶���ˮƽ����v1=![]() ��
��
����������ֱ�������ȼ���ֱ���˶������ٶ�Ϊa�����糡ʱ��ֱ�����ٶ�Ϊv2
��ֱ����a=![]() v2=at ��
v2=at ��
�ɼ��ι�ϵ��tan��=![]() ��
��
�������ݽ�ã�E=10000V/m ��
��3����������ӽ��ų�ʱ���ٶȴ�СΪv��
��v=![]() ��
��
�������ݽ�ã�v=2��104m/s ��
�������˶��ĶԳ��Կ�֪�������ٶȷ�����ų�����Բ�ģ�
������ٶȷ����ӳ��߹��ų�����Բ�ģ������ڴų��е��˶��켣��ͼ��ʾ
��켣�뾶Ϊ��r=Rtan60�㣬��ã�r=0.3m ��
��ţ�ٵڶ����ɵã�qvB=m![]() ��
��
�������ݽ�ã�B=0.13T �⣻
�𣺣�1����������U1=100V�ĵ糡���ٺ������Ϊ1��104m/s��
��2�����������ƫת�糡�ĵ糡ǿ��EΪ10000V/m��
��3����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�СΪ0.13T��






