题目内容
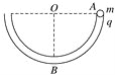
【题目】如图所示,一个质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点。已知圆弧的半径为R且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力。求:
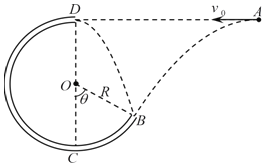
(1)小球从A点做平抛运动的初速度v0的大小;
(2)小球在D点时的速度大小;
(3)在D点处小球对管壁的作用力的大小和方向。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,方向竖直向下
,方向竖直向下
【解析】
根据几何关系求出平抛运动下降的高度,从而求出竖直方向上的分速度,根据运动的合成和分解求出初速度的大小;根据平抛运动知识求出小球在D点的速度,再根据牛顿第二定律求出管壁对小球的弹力作用。
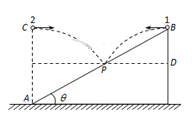
(1) 小球从A到B的过程做平抛运动。如图所示,

由几何关系可得
![]()
![]()
联立解得:![]() ;
;
(2) 小球从D到B的过程做平抛运动
![]()
解得:![]() ;
;
(3) D处小球做圆周运动,设管壁对小球的支持力为![]() ,由牛顿第二定律有
,由牛顿第二定律有
![]()
解得:![]()
由牛顿第三定律可得,小球在D处对管壁的压力大小为![]() ,方向竖直向下。
,方向竖直向下。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目