题目内容
(15分)如图所示，在A点固定一正电荷，电量为Q，在离A高度为H的C处由静止释放某带同种电荷的液珠，开始运动瞬间的加速度大小恰好为重力加速度g。已知静电常量为k，两电荷均可看成点电荷，不计空气阻力。求：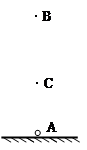
(1)液珠的比荷
(2)液珠速度最大时离A点的距离h。
(3)若已知在点电荷Q的电场中，某点的电势可表示成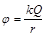
，其中r为该点到Q的距离（选无限远的电势为零）。求液珠能到达的最高点B离A点的高度rB。
(1) q/m=2gh2/kQ (2) h= 
H (3) rB=2H
解析试题分析：(1) 设液珠的电量为q,质量为m,由题意知，当液珠在C点时
kQq/H2-mg=mg 比荷为q/m=2gh2/kQ
(2)当液珠速度最大时，kQq/h2=mg
得 h=H
(3) 设BC间的电势差大小UCB,由题意得
UCB=φC-φB=kQ/H-kQ/rB
对由释放至液珠到达最高点(速度为零)的全过程应用动能定理得
qUCB-mg(rB-H)=0
即 q(kQ/H-kQ)/rB -mg(rB-H)=0
将第(1)问的结果代入化简 rB2-3HrB+2H2=0
解得： rB=2H rB′=H(舍去)
考点：本题考查牛顿第二定律、电势差与电势大小关系、电场力做功的应用。
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
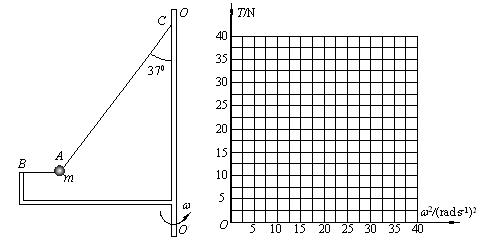
时，细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°，求角速度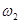
时，细线AB刚好竖直，且张力为0，求此时角速度
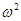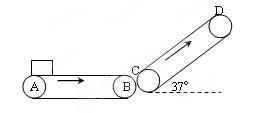
变化的关系图像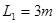
；另一台倾斜传送，传送带与地面间的倾角
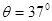，C、D两端相距
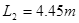，B、C相距很近。水平传送带以
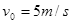沿顺时针方向转动。现将质量为
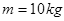的一袋大米无初速度的放在A端，它随传送带到达B点后，速度大小不变的传到倾斜传送带的C端。米袋与两传送带之间的动摩擦因素均为
，取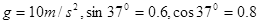
。
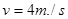的速率沿顺时针方向转动，则米袋从C端运动到D端的时间为多少？
，AB段和CD段通过极短的BC段平滑连接．现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h．稳定工作时传送带速度保持不变，始终为v，CD段上各箱等距排列，相邻两箱的距离为L．每个箱子在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段时的微小滑动）．传送带由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦．
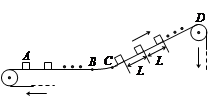
。圆形轨道是光滑的，水平轨道足够长。取重力加速度g=10m/s2。求：
;