题目内容
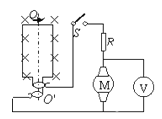
【题目】如图所示，有一可绕竖直中心轴转动的水平圆盘，上面放置劲度系数为k=46N/m的弹簧，弹簧的一端固定于轴O点，另一端连接质量为m=1kg的小物块A，物块与盘间的动摩擦因数为μ=0.2，开始时弹簧未发送形变，长度为
，若最大静摩擦力与滑动摩擦力大小相等，重力加速度
，物块A始终与圆盘一起转动，则：
（1）圆盘的角速度多大时，物块A将开始滑动？
（2）当角速度缓慢地增加到4rad/s时，弹簧的伸长量是多少？(弹簧伸长在弹性限度内且物块未脱离圆盘)。
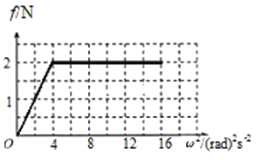
（3）在角速度从零缓慢地增加到4rad/s过程中，物块与盘间摩擦力大小为f，试通过计算在坐标系中作出
图像。
【答案】（1）
（2）
（3）如图所示
【解析】
试题分析：（1）设盘的角速度为
时，物块A将开始滑动，此时物块的最大静摩擦力提供向心力，则有：
，解得：
，
（2）设此时弹簧的伸长量为
，物块受到的摩擦力和弹簧的弹力的合力提供向心力，则有：
，代入数据解得：
（3）在角速度从零缓慢地增加到2rad/s过程中，物块与盘间摩擦力为静摩擦力
，f∝ω2，f随着角速度平方的增加而增大；
当
时，物块与盘间摩擦力为滑动摩擦力为定值，为
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
