题目内容
如图所示，螺线管横截面积为S，线圈匝数为N，电阻为R1，管内有水平向左的变化磁场。螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内，与水平面的夹角为q，两导轨间距为L。导轨电阻忽略不计。导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中。金属杆ab垂直导轨，杆与导轨接触良好，并可沿导轨无摩擦滑动。已知金属杆ab的质量为m，电阻为R2，重力加速度为g。忽略螺线管磁场对金属杆ab的影响、忽略空气阻力。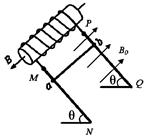
（1）为使ab杆保持静止，求通过ab的电流的大小和方向；
（2）当ab杆保持静止时，求螺线管内磁场的磁感应强度B的变化率；
（3）若螺线管内方向向左的磁场的磁感应强度的变化率DB/Dt＝k（k＞0）。将金属杆ab由静止释放，杆将沿斜面向下运动。求当杆的速度为v时，杆的加速度大小。
（1）
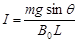，电流方向为由b到a（2）
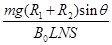（3）
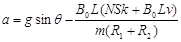
解析试题分析：（1）以金属杆ab为研究对象，根据平衡条件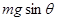 
- B0I L＝0（1分）
得 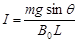（1分）
通过ab杆电流方向为由b到a（或在图中标出） （1分）
（2）根据法拉第电磁感应定律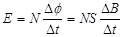 
（1分）
根据欧姆定律 
（1分）
得：
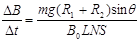（1分）
（3）根据法拉第电磁感应定律
（1分）
ab杆切割磁感线产生的电动势 E2 ＝ B0Lv （1分）
总电动势 E总 ＝ E1 + E2
感应电流 
（1分）
根据牛顿第二定律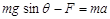 
（1分）
安培力 F ＝ B0 I′L （1分）
所以 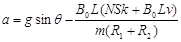（1分）
考点：考查了法拉第电磁感应定律，牛顿第二定律
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的
光滑圆弧形固定轨道接触（但不粘连），木板的右端到竖直墙的距离为s；另一质量为2m的小滑块从轨道的最高点由静止开始下滑，从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。已知滑块与长木板间的动摩擦因数为μ。试求：
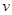与s的关系；
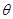的光滑斜面固定在水平面上，水平虚线L下方有垂直于斜面向下的匀强磁场，磁感应强度为B．正方形闭合金属线框边长为h，质量为m，电阻为R，放置于L上方一定距离处，保持线框底边ab与L平行并由静止释放，当ab边到达L时，线框速度为
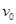. ab边到达L下方距离d处时，线框速度也为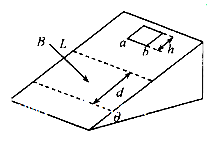
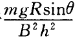
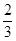T、方向垂直xoy平面向里，在x轴上方11cm处放置一个与x轴平行的光屏。已知A、B两板间电压UAB＝100V, C、D两板间电压 UCD="300V," 偏转电场极板长L=4cm，两板间距离d="6cm," 磁场圆心坐标为（6，0）、半径R＝3cm。现有带正电的某种粒子从A极板附近由静止开始经电场加速，穿过B板沿C、D两板间中心线y = 8cm进入偏转电场，由y轴上某点射出偏转电场，经磁场偏转后打在屏上。带电粒子比荷
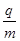=106c/kg，不计带电粒子的重力。求：
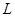，连线与坐标轴＋y方向的夹角为
= 370，不计粒子的重力。（sin37o=0．6，cos37o=0．8)
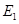中，粒子沿＋y方向从O点射出，恰好经过A点；若在平行于y轴正方向的匀强电场
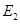中，粒子沿＋x方向从O点射出，也恰好能经过A点，求这两种情况电场强度的比值