题目内容
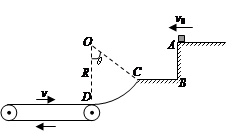
如图所示，在y轴左侧放置一加速电场和偏转电场构成的发射装置，C、D两板的中心线处于y=8cm的直线上；右侧圆形匀强磁场的磁感应强度大小为B=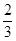
T、方向垂直xoy平面向里，在x轴上方11cm处放置一个与x轴平行的光屏。已知A、B两板间电压UAB＝100V, C、D两板间电压 UCD="300V," 偏转电场极板长L=4cm，两板间距离d="6cm," 磁场圆心坐标为（6，0）、半径R＝3cm。现有带正电的某种粒子从A极板附近由静止开始经电场加速，穿过B板沿C、D两板间中心线y = 8cm进入偏转电场，由y轴上某点射出偏转电场，经磁场偏转后打在屏上。带电粒子比荷
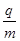=106c/kg，不计带电粒子的重力。求：
（1）该粒子射出偏转电场时速度大小和方向；
（2）该粒子打在屏上的位置坐标；
（3）若将发射装置整体向下移动，试判断粒子能否垂直打到屏上？若不能，请简要说明理
由。若能，请计算该粒子垂直打在屏上的位置坐标和发射装置移动的距离。
（1）
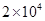m/s，速度方向与x轴正方向夹角
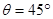（2）（17cm,11cm）（3）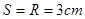
解析试题分析：⑴ 电场加速：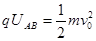
（1分）
电场偏转：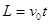
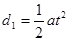（1分）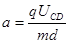
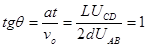（1分） 
（1分）
速度大小
m/s （1分）
速度方向与x轴正方向夹角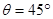 （1分）
⑵如图所示，粒子与y轴负方向成45°进入第一象限，做匀速运动，进入磁场后做匀速圆周运动，运动四分之一周，出磁场后做匀速运动。由对称关系，粒子射出磁场时速度与x轴正方向成45° （2分）
y =11cm （1分）
x = 6cm+11cm=17cm （1分）
打在屏上的位置坐标（17cm,11cm） （1分）
⑶可以垂直打在屏上。 （1分）
粒子在磁场中: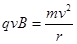
轨道半径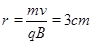 
（1分）
根据磁聚集原理，带电粒子在磁场中的轨道半径与圆形匀强磁场的半径R相等时，带电粒子必会聚于同一点，会聚的位置与粒子入射方向相垂直的直径的端点，即为如图所示的N点。 （1分）
假设粒子可以垂直打在屏上。由几何关系得，垂直打到屏的位置坐标：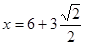
cm ，y =11cm，位置坐标为（
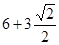,11） （1分）
因要求粒子垂直打到屏，则射出磁场时的速度方向与x轴垂直，此时粒子的轨道半径与x轴平行，从而推得射入磁场时的位置为x轴的M点（菱形对边平行且相等）。
向下移动的距离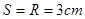（等腰梯形的两腰相等） （2分）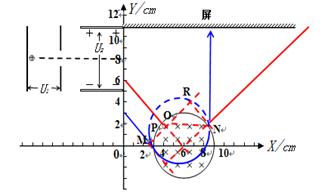
考点：考查了牛顿第二定律与电磁场综合应用
阅读快车系列答案
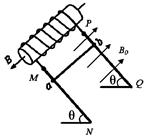
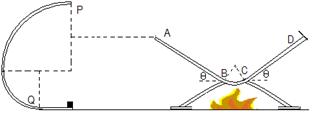
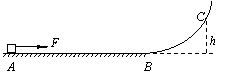
，AB=CD=2R，A、D等高，D端固定一小挡板，碰撞不损失机械能。滑块的运动始终在包括锅底最低点的竖直平面内，重力加速度为g。
