题目内容
（15）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，Y轴为两种场的分界面，图中虚线为磁场区域的右边界，现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置(-L，0)处，以初速度v0沿x轴正方向开始运动，且已知L = (重力不计)，试求：使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d 应满足的条件．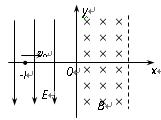
d＜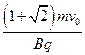
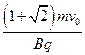
带电粒子在电场中做类平抛运动，设运动的加速度为a．由牛顿运动定律得:qE = ma设粒子出电场、入磁场时速度的大小为v，此时在Y轴方向的分速度为vy，粒子在电场中运动的时间为t．
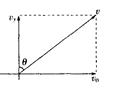
则有: vy=at l=v0t
解得:，vy= v0 v =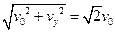
（
４分）
设v的方向与y轴夹角为θ,则有cosθ=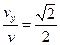
得θ=450.（4分）
粒子进入磁场后在洛伦兹力作用下做圆周运动，如图所示，
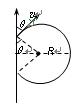
则有 :qvB =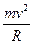
可得：R= 
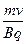（4分）
要使粒子穿越磁场区域，磁场的宽度应满足的条件d＜R(1+ cosθ)
结合已知条件解以上各式可得: d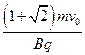＜（３分）
则有: vy=at l=v0t
解得:，vy= v0 v =
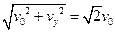（４分）设v的方向与y轴夹角为θ,则有cosθ=
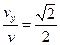得θ=450.（4分）粒子进入磁场后在洛伦兹力作用下做圆周运动，如图所示，
则有 :qvB =
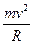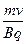可得：R= （4分）要使粒子穿越磁场区域，磁场的宽度应满足的条件d＜R(1+ cosθ)
结合已知条件解以上各式可得: d＜
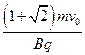（３分）
练习册系列答案
名校课堂系列答案
相关题目
，两侧为相同的匀强磁场，方向垂直纸面向里。一质量为
、带电量
、重力不计的带电粒子，以初速度
垂直边界射入磁场做匀速圆周运动，后进入电场做匀加速运动，然后第二次进入磁场中运动，此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍，第三次是第一次的三倍，以此类推。求
。
次经过电场时电场强度的大小
。
。
面内建立如图所示的直角坐标系，将第I、第II象限合称为区域一，第III、IV象限合称为区域二，其中一个区域内有大小、方向均未标明的匀强电场，另一个区域内有大小为 2×10－2T、方向垂直于水平桌面的匀强磁场．把一个比荷为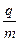
=2×108C／kg的正电荷从坐标为(0，－1)的A点处由静止释放，电荷以一定的速度沿直线AC运动并从坐标为(1，0)的C点第一次经x轴进入区域一，经过一段时
间，从坐标原点O再次回到区域二（重力不计）。
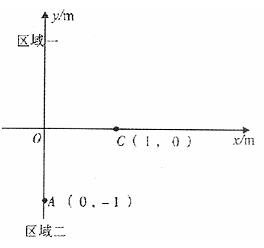
)，由于磁场位置的不同，导致粒子打在荧光屏上的位置也不同，求粒子打在荧光屏上点的纵坐标的范围。
