题目内容
在水平光滑的绝缘桌 面内建立如图所示的直角坐标系,将第I、第II象限合称为区域一,第III、IV象限合称为区域二,其中一个区域内有大小、方向均未标明的匀强电场,另一个区域内有大小为 2×10-2T、方向垂直于水平桌面的匀强磁场.把一个比荷为
面内建立如图所示的直角坐标系,将第I、第II象限合称为区域一,第III、IV象限合称为区域二,其中一个区域内有大小、方向均未标明的匀强电场,另一个区域内有大小为 2×10-2T、方向垂直于水平桌面的匀强磁场.把一个比荷为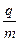 =2×108C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度沿直线AC运动并从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时
=2×108C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度沿直线AC运动并从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时 间,从坐标原点O再次回到区域二(重力不计)。
间,从坐标原点O再次回到区域二(重力不计)。
(1)指出哪个区域是电场、哪个区域是磁场以及电场和磁场的方向;
(2)求电荷在磁场里作匀速圆周运动的轨道半径r和匀强电场强度E的大小;
(3)求从释放到第二次经过x轴电荷运动的时间t。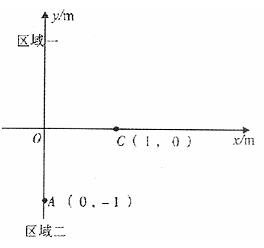
 面内建立如图所示的直角坐标系,将第I、第II象限合称为区域一,第III、IV象限合称为区域二,其中一个区域内有大小、方向均未标明的匀强电场,另一个区域内有大小为 2×10-2T、方向垂直于水平桌面的匀强磁场.把一个比荷为
面内建立如图所示的直角坐标系,将第I、第II象限合称为区域一,第III、IV象限合称为区域二,其中一个区域内有大小、方向均未标明的匀强电场,另一个区域内有大小为 2×10-2T、方向垂直于水平桌面的匀强磁场.把一个比荷为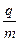 =2×108C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度沿直线AC运动并从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时
=2×108C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度沿直线AC运动并从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时 间,从坐标原点O再次回到区域二(重力不计)。
间,从坐标原点O再次回到区域二(重力不计)。(1)指出哪个区域是电场、哪个区域是磁场以及电场和磁场的方向;
(2)求电荷在磁场里作匀速圆周运动的轨道半径r和匀强电场强度E的大小;
(3)求从释放到第二次经过x轴电荷运动的时间t。

(1)区域一是磁场,方向垂直纸面向里。区域二是电场,方向由A指向C。 (4分)
(2)设电场强度的大小为E,电荷从C点进入
区域I的速度为v。
电荷从A到C做初速度为零的匀加速直线运动,
且过C点时速度方向与x轴正方向成45°角, (1分)
AC间距离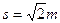 ,则: (1分)
,则: (1分)
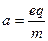 …………① (1分)
…………① (1分)
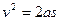 …………② (1分)
…………② (1分)
电荷进入区域I后,在洛仑兹力的作用下做
匀速圆周运动,运动轨迹如图,则:
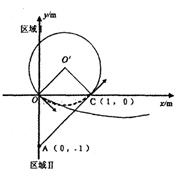
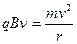 ………………③ (2分)
………………③ (2分)
由题意及几何关系: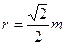 …………④ (1分)
…………④ (1分)
由①②③④可得: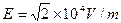 (1分)
(1分)
(3)由A到C得,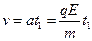 (1分)
(1分)
代入数据得t1=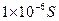 (1分)
(1分)
由C到O得,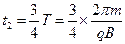 (1分)
(1分)
代入数据得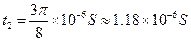 (1分)
(1分)
所以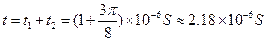 (1分)
(1分)
(2)设电场强度的大小为E,电荷从C点进入
区域I的速度为v。
电荷从A到C做初速度为零的匀加速直线运动,
且过C点时速度方向与x轴正方向成45°角, (1分)
AC间距离
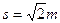 ,则: (1分)
,则: (1分)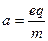 …………① (1分)
…………① (1分)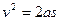 …………② (1分)
…………② (1分)电荷进入区域I后,在洛仑兹力的作用下做
匀速圆周运动,运动轨迹如图,则:

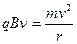 ………………③ (2分)
………………③ (2分)由题意及几何关系:
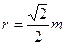 …………④ (1分)
…………④ (1分)由①②③④可得:
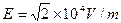 (1分)
(1分)(3)由A到C得,
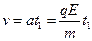 (1分)
(1分)代入数据得t1=
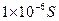 (1分)
(1分)由C到O得,
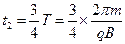 (1分)
(1分)代入数据得
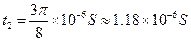 (1分)
(1分)所以
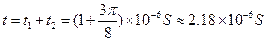 (1分)
(1分)略

练习册系列答案
相关题目

 ,忽略粒子重力及阻力的影响。
,忽略粒子重力及阻力的影响。
 产生的初速度为零、带电量均为
产生的初速度为零、带电量均为 、质量不同的正离子,被电压为
、质量不同的正离子,被电压为 的加速电场加速后匀速通过准直管,在到两极板等距离处垂直射入平行板间的匀强偏转电场,平行板间的电压为
的加速电场加速后匀速通过准直管,在到两极板等距离处垂直射入平行板间的匀强偏转电场,平行板间的电压为 .偏转后通过极板
.偏转后通过极板 上的小孔
上的小孔 离开电场.经过一段匀速直线运动,垂直于边界
离开电场.经过一段匀速直线运动,垂直于边界 进入磁感强度大小为
进入磁感强度大小为 、方向垂直于纸面向外的匀强磁场,已知
、方向垂直于纸面向外的匀强磁场,已知 .(忽略粒子所受重力)
.(忽略粒子所受重力) 的正离子在磁场中做圆周运动的半径;
的正离子在磁场中做圆周运动的半径; 的中点
的中点 处,试求能打在边
处,试求能打在边

 平面内,第Ⅲ象限的直线
平面内,第Ⅲ象限的直线 是电场与磁场的边界,
是电场与磁场的边界, 轴负方向成
轴负方向成 角.在
角.在 且
且 ,场强大小
,场强大小 ,在
,在 且
且 ,磁感应强度大小为
,磁感应强度大小为 ,如图所示.一不计重力的带负电微粒,从坐标原点O沿
,如图所示.一不计重力的带负电微粒,从坐标原点O沿 轴负方向以
轴负方向以 的初速度进入磁场,已知微粒的电荷量
的初速度进入磁场,已知微粒的电荷量 ,质量为
,质量为 ,
, 求:
求:

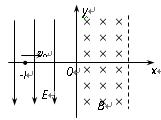
 且斜向上方.现有一质量为m、电荷量为q的正离子,以速度
且斜向上方.现有一质量为m、电荷量为q的正离子,以速度 由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点进入电场区域,该离子经过C点时的速度方向与x轴夹角为
由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点进入电场区域,该离子经过C点时的速度方向与x轴夹角为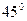 .不计离子的重力,设磁场区域和电场区域足够大.
.不计离子的重力,设磁场区域和电场区域足够大. 小题1:C点的坐标.
小题1:C点的坐标.