题目内容
A、B两列火车在同一轨道上通向行驶,A车在前,速度为va=10m/s,B车在后速度为vb=30m/s因大雾能见度低,B车在距A车
600m时,才发现前方有A车,这时B车立即刹车,但要经过180m的距离B车才能停止.问
(1)B车刹车时的加速度大小为多少?
(2)A车若按原速前进,两车是否相撞,若会相撞,将在何时何地发生?
(3)B车在刹车的同时发出信号,A车在司机受到信号2s后加速前进,求A车的加速度满足什么条件才能避免事故发生?(不计信号传输时间)
600m时,才发现前方有A车,这时B车立即刹车,但要经过180m的距离B车才能停止.问
(1)B车刹车时的加速度大小为多少?
(2)A车若按原速前进,两车是否相撞,若会相撞,将在何时何地发生?
(3)B车在刹车的同时发出信号,A车在司机受到信号2s后加速前进,求A车的加速度满足什么条件才能避免事故发生?(不计信号传输时间)
分析:判断两车是否相撞:当两车速度相等是相撞与否的关键点,假设后车B车速度减到与前车A速度相等时还不相撞,在以后的时间里,后车速度小于前车,以后永不相撞.
解答:解:(1)B刹车后要经过180m距离才能停下,
由位移速度公式 vt2-v02=2ax
解得:B的加速度 aB=-0.25m/s2
B车刹车时的加速度大小为0.25m/s2
(2)设经过时间t,两车的速度相等,
即:vB+at=vA
解得:t=80s
此时A的位移xA=vAt=800m
B的位移xB=vBt+
aBt2=1600>xA+600=1400
所以两车会相撞.
设两车相撞的时间为t1,两车相撞时有xB=xA+600
即:vBt1+
aB
=vAt1+600
解得:t=40s
此过程A车前进距离 xA=vAt1=400m
即在B车发现A车后40s,A车向前行驶了400m即被B车撞了.
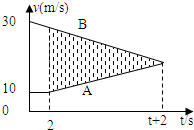
(3)作v-t图如图,设A的加速度为aA,由题意可算出2秒末内A、B间的距离为:
d1=600-(30-10)×2+
×0.25×22=560.5m
 在2秒末B的速度为vB1=30-0.25×2=29.5m/s
在2秒末B的速度为vB1=30-0.25×2=29.5m/s
设再过时间t两车的速度相等,且B车未与A车相撞,所以有:
速度关系:vB+aB(t+2)=vA+aAt 即(4aA+1)t=78
位移关系:xB≤xA+560.5 反映在图象上就是阴影部分三角形的面积为
S≤560.5
即:
(29.5-10)t≤560.5 解得t≤57.5s
代入(4aA+1)t=78
解得aA≥0.09 m/s2
答:B车刹车时的加速度大小为0.25m/s2;B车发现A车后40s,A车向前行驶了400m即被B车撞了;A车的加速度aA≥0.09 m/s2才能避免事故发生.
由位移速度公式 vt2-v02=2ax
解得:B的加速度 aB=-0.25m/s2
B车刹车时的加速度大小为0.25m/s2
(2)设经过时间t,两车的速度相等,
即:vB+at=vA
解得:t=80s
此时A的位移xA=vAt=800m
B的位移xB=vBt+
| 1 |
| 2 |
所以两车会相撞.
设两车相撞的时间为t1,两车相撞时有xB=xA+600
即:vBt1+
| 1 |
| 2 |
| t | 2 1 |
解得:t=40s
此过程A车前进距离 xA=vAt1=400m
即在B车发现A车后40s,A车向前行驶了400m即被B车撞了.
(3)作v-t图如图,设A的加速度为aA,由题意可算出2秒末内A、B间的距离为:
d1=600-(30-10)×2+
| 1 |
| 2 |
 在2秒末B的速度为vB1=30-0.25×2=29.5m/s
在2秒末B的速度为vB1=30-0.25×2=29.5m/s设再过时间t两车的速度相等,且B车未与A车相撞,所以有:
速度关系:vB+aB(t+2)=vA+aAt 即(4aA+1)t=78
位移关系:xB≤xA+560.5 反映在图象上就是阴影部分三角形的面积为
S≤560.5
即:
| 1 |
| 2 |
代入(4aA+1)t=78
解得aA≥0.09 m/s2
答:B车刹车时的加速度大小为0.25m/s2;B车发现A车后40s,A车向前行驶了400m即被B车撞了;A车的加速度aA≥0.09 m/s2才能避免事故发生.
点评:追及问题解题关键:①掌握好两个关系:时间关系和位移关系②一个条件:两者速度相等,这往往是能否追上,或两者距离最大、最小的临界条件是分析问题的切入点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目