题目内容
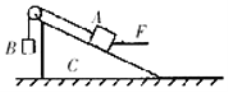
【题目】如图传送装置, 水平传送带ab 在电机的带动下以恒定速率ν= 4m/s 运动,在传送带的右端点a无初速的轻放一个质量 m=1kg 的物块( 视为质点), 当物块 A 到达传送带左端点 b 点时, 即刻再在a 点无初速度轻放另一质量为2m 的物块 B( 视为质点). 两物块到达 b 点时都恰好与传送带等速, 在 b 端点的左方为一个水平放置的长直轨道 cd, 轨道上静止停放着质量 m 的木板 C, 从 b 点滑出的物块恰能水平滑上(无能量损失)木板上表面, 木板足够长. 已知: 物块与传送带间的动摩擦因数 1 =0.8,与木板间的动摩擦因数 2 =0.2; 木板与轨道间的动摩擦因数 3 =0.1; 设最大静摩擦力等于滑动摩擦力, 取g=10m/s2. 试求:
(1)物块 A、 B 滑上木板 C 上的时间差t;
(2)木板 C 运动的总时间.
(3)木板 C 与轨道间的摩擦生热 Q.

【答案】(1)0.5s;(2)2.75s;(3)9.75J;
【解析】(1)物块在传送带上的加速时间即为滑上木板的时间差,设AB在传送带上加速度为a0,μ1mg=ma0,解得a0=8m/s2
![]() 解得t=0.5s
解得t=0.5s
(2)过程一:A物块滑上木板C与木板有相对运动,μ2mg=maA,aA=2m/s2,方向向右;
木板C水平方向受力:μ2mg=μ32mg,木板C保持静止;
过程二:经过t=0.5s后B物块滑上木板C,此时A速度:vA=v-aAt=3m/s;
B物块和木板C有相对运动:μ22mg=2maB,aB=2m/s2,
木板C: ![]() 解得aC=2m/s2
解得aC=2m/s2
木板C由静止开始向左做匀加速运动:A与C共速:vA-aAt1=aCt1
解得t1=0.75s,vAC=1.5M/S此时vB=v-aBt1=2.5m/s
过程三:物块B相对木板C继续向左运动,仍做aB=2m/s2的匀减速运动;木板C和物块A保持相对静止,将木板C和物块A看做整体,则: ![]() ,
,
解得aAC=0
故木板C和物体A向左做匀速直线运动,直到ABC共速为:vB-aBt2=vAC
解得t2=0.5s
过程四:三物体保持相对静止,一起做匀减速运动直到速度减为0木板停止运动,则:
![]() ,解得aABC=1m/s2
,解得aABC=1m/s2
![]()
故木板运动的总时间:t=t1+t2+t3=2.75s
(3)过程二中木板的位移: ![]()
过程三中木板的位移: ![]()
过程四中木板的位移: ![]()
木板与轨道的摩擦生热: ![]()