题目内容
位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0 m,bd长L2=0.5 m,线框的质量m=0.2 kg,电阻R=2 Ω.其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行.两边界间距离为H,H>L2,磁场的磁感应强度B=1.0 T,方向与线框平面垂直。如图27所示,令线框的dc边从离磁场区域上边界PP′的距离为h=0.7 m处自由下落.已知线框的dc边进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已达到这一阶段的最大值.问从线框开始下落,到dc边刚刚到达磁场区域下边界QQ′的过程中,磁场作用于线框的安培力所做的总功为多少?(g取10 m/s2)

【答案】
-0.8 J
【解析】本题中重力势能转化为电能和动能,而安培力做的总功使重力势能一部分转化为电能,电能的多少等于安培力做的功.
依题意,线框的ab边到达磁场边界PP′之前的某一时刻线框的速度达到这一阶段速度最大值,以v0表示这一最大速度,则有
E=BL1v0
线框中电流 I=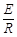 =
=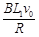
作用于线框上的安培力 F=BL1I=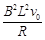
速度达到最大值条件是 F=mg
所以v0=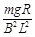 =4 m/s.
=4 m/s.
dc边继续向下运动过程中,直至线框的ab边达到磁场的上边界PP′,线框保持速度v0不变,故从线框自由下落至ab边进入磁场过程中,由动能定理得:
mg(h+L2)+W安=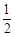 mv
mv
W安=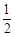 mv
mv -mg(h+L2)=-0.8 J
-mg(h+L2)=-0.8 J
ab边进入磁场后,直到dc边到达磁场区下边界QQ′过程中,作用于整个线框的安培力为零,安培力做功也为零,线框只在重力作用下做加速运动,故线框从开始下落到dc边刚到达磁场区域下边界QQ′过程中,安培力做的总功即为线框自由下落至ab边进入磁场过程中安培力所做的功
W安=-0.8 J
负号表示安培力做负功.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
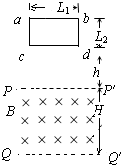 位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0m,bd长L2=0.5m,线框的质量m=0.2kg,电阻R=2Ω.其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行,两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域的上边界PP′的距离为h=0.7m处自由下落,已知在线框的dc边进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已达到这一阶段的最大值.试求:
位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0m,bd长L2=0.5m,线框的质量m=0.2kg,电阻R=2Ω.其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行,两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域的上边界PP′的距离为h=0.7m处自由下落,已知在线框的dc边进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已达到这一阶段的最大值.试求: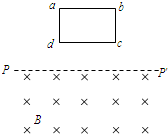 (2006?海淀区二模)如图所示,位于竖直平面内的矩形平面单匝导线框abcd,其下方有一匀强磁场区域,该区域的上边界PP′水平,并与线框的ab边平行,磁场方向与线框平面垂直.已知磁场的磁感应强度为B,线框ab边长为L1,ad边长为L2,线框质量为m.令线框的dc边从离磁场区域边界PP′的高度为h处由静止开始下落,线框刚好匀速进入磁场区域.
(2006?海淀区二模)如图所示,位于竖直平面内的矩形平面单匝导线框abcd,其下方有一匀强磁场区域,该区域的上边界PP′水平,并与线框的ab边平行,磁场方向与线框平面垂直.已知磁场的磁感应强度为B,线框ab边长为L1,ad边长为L2,线框质量为m.令线框的dc边从离磁场区域边界PP′的高度为h处由静止开始下落,线框刚好匀速进入磁场区域.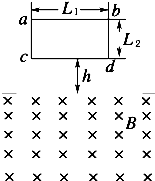 位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0m,bd长L2=0.5m,线框的质量m=0.2kg,电阻R=2Ω.其下方有一较大匀强磁场区域,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界的距离为h=0.7m处自由下落.已知线框的dc边进入磁场以后,ab边到达边界之前的某一时刻线框的速度已达到这一阶段的最大值.从线框开始下落,到ab边完全进入磁场的过程中(g取10m/s2),求
位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0m,bd长L2=0.5m,线框的质量m=0.2kg,电阻R=2Ω.其下方有一较大匀强磁场区域,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界的距离为h=0.7m处自由下落.已知线框的dc边进入磁场以后,ab边到达边界之前的某一时刻线框的速度已达到这一阶段的最大值.从线框开始下落,到ab边完全进入磁场的过程中(g取10m/s2),求