题目内容
 如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的直径分别为24.75cm、8.25cm、66cm,则当人踩踏脚板使自行车以3.3m/s的速度在平直的水平路面上匀速前进时,求:
如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的直径分别为24.75cm、8.25cm、66cm,则当人踩踏脚板使自行车以3.3m/s的速度在平直的水平路面上匀速前进时,求:(1)后轮C的角速度;
(2)牙盘A的边缘D点的线速度.
分析:(1)根据公式v=ωr求解后轮转动的角速度;
(2)自行车的链条不打滑,牙盘A的边缘D点的线速度与飞轮边缘的线速度大小相等,由v=ωr列式求解.
(2)自行车的链条不打滑,牙盘A的边缘D点的线速度与飞轮边缘的线速度大小相等,由v=ωr列式求解.
解答:解:(1)根据公式v=ωr,后轮的角速度为:ω=
=
=10rad/s;
(2)飞轮角速度与后轮角速度相同,也为10rad/s;
故飞轮的线速度为:v′=ωr=10rad/s×
×0.0825m=0.2125m/s;
自行车的链条不打滑,牙盘A的边缘D点的线速度与飞轮边缘的线速度大小相等,也为0.2125m/s;
答:(1)后轮C的角速度为10rad/s;
(2)牙盘A的边缘D点的线速度为0.2125m/s.
| v |
| R |
| 3.3m/s |
| 33×0.01m |
(2)飞轮角速度与后轮角速度相同,也为10rad/s;
故飞轮的线速度为:v′=ωr=10rad/s×
| 1 |
| 2 |
自行车的链条不打滑,牙盘A的边缘D点的线速度与飞轮边缘的线速度大小相等,也为0.2125m/s;
答:(1)后轮C的角速度为10rad/s;
(2)牙盘A的边缘D点的线速度为0.2125m/s.
点评:本题关键明确同缘传动边缘点线速度相等,同轴传递角速度相等,然后结合线速度与角速度公式v=ωr列式求解.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
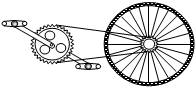 如图所示是自行车传动装置的示意图,若脚蹬匀速转一圈需要时间T,已数出大齿轮齿数为48,小齿轮齿数为16,自行车后轮半径R.下列说法中正确的是( )
如图所示是自行车传动装置的示意图,若脚蹬匀速转一圈需要时间T,已数出大齿轮齿数为48,小齿轮齿数为16,自行车后轮半径R.下列说法中正确的是( )| A、小齿轮、大齿轮边缘点的线速度大小之比vA:vB=3:1 | B、小齿轮、大齿轮的角速度大小之比ωA:ωB=1:3 | C、小齿轮、大齿轮的周期之比TA:TB=1:1 | D、自行车前进速度为6πR/T |
 如图所示是自行车传动装置的示意图.假设踏脚板每2s转一圈,要知道在这种情形下自行车前进的速度有多大,还需测量哪些量?
如图所示是自行车传动装置的示意图.假设踏脚板每2s转一圈,要知道在这种情形下自行车前进的速度有多大,还需测量哪些量? 如图所示是自行车传动装置的示意图,若脚蹬匀速转一圈需要时间T,已数出链轮齿数为48,飞轮齿数为16,要知道在此情况下自行车前进的速度,还需要测量的物理量是
如图所示是自行车传动装置的示意图,若脚蹬匀速转一圈需要时间T,已数出链轮齿数为48,飞轮齿数为16,要知道在此情况下自行车前进的速度,还需要测量的物理量是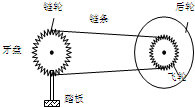 如图所示是自行车传动装置的示意图.如果踏板转一圈需要时间T,要知道在这种情况下自行车前进的速度有多大,需要测量的物理量有:牙盘半径R,飞轮半径r和
如图所示是自行车传动装置的示意图.如果踏板转一圈需要时间T,要知道在这种情况下自行车前进的速度有多大,需要测量的物理量有:牙盘半径R,飞轮半径r和