题目内容
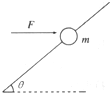 如图所示,质量为lkg的小球穿在斜杆上,斜杆与水平方向的夹角为θ=300,球恰好能在杆上匀速滑动.若球受到一大小为F=20N的水平推力作用,可使小球沿杆向上加速滑动,求:
如图所示,质量为lkg的小球穿在斜杆上,斜杆与水平方向的夹角为θ=300,球恰好能在杆上匀速滑动.若球受到一大小为F=20N的水平推力作用,可使小球沿杆向上加速滑动,求:(1)画出小球在杆上匀速滑动时的受力分析图.
(2)小球与斜杆间的滑动摩擦因数μ的大小.
(3)小球沿杆向上加速滑动时的加速度大小.
分析:球恰好能在杆上匀速滑动,说明小球受力平衡,对小球进行受力分析即可求解;水平推力作用后,由牛顿第二定律及滑动摩擦力公式即可求解.
解答:解:(1)小球在杆上匀速滑动时的受力分析,如图所示:
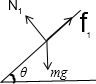
(2)小球在杆上匀速滑动时,由平衡条件可知:
平行于杆方向:mgsinθ=f1
y轴方向:N1=mgcosθ
f1=μN1
解得小球与斜杆间的动摩擦因数μ=tan30°=
(3)水平推力作用后,小球受力如图所示:
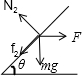
由牛顿第二定律:
Fcosθ-mgsinθ-f2=ma
f2=μN2=μ(Fsinθ+mgcosθ)
解得小球沿杆向上加速滑动的加速度:a=
-10=1.55m/s2
答:(1)小球在杆上匀速滑动时的受力分析如(1)图.
(2)小球与斜杆间的滑动摩擦因数为
(3)小球沿杆向上加速滑动时的加速度大小为1.55m/s2

(2)小球在杆上匀速滑动时,由平衡条件可知:
平行于杆方向:mgsinθ=f1
y轴方向:N1=mgcosθ
f1=μN1
解得小球与斜杆间的动摩擦因数μ=tan30°=
| ||
| 3 |
(3)水平推力作用后,小球受力如图所示:

由牛顿第二定律:
Fcosθ-mgsinθ-f2=ma
f2=μN2=μ(Fsinθ+mgcosθ)
解得小球沿杆向上加速滑动的加速度:a=
20
| ||
| 3 |
答:(1)小球在杆上匀速滑动时的受力分析如(1)图.
(2)小球与斜杆间的滑动摩擦因数为
| ||
| 3 |
(3)小球沿杆向上加速滑动时的加速度大小为1.55m/s2
点评:本题考查了牛顿第二定律和力的合成与分解相关知识点,求解加速度是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 如图所示,滑块A的质量m=0.05kg,与水平地面间的动摩擦因数μ=0.2,用长度不等的细线悬挂的若干个小球,质量均为m=0.05kg,沿x轴排列,且小球与地面间无弹力。滑块A与第1只小球及相邻两小球间距离均为s=2m,细线长分别为L1、L2、L3……(图中只画三只小球,滑块、小球可视为质点)。开始时,滑块A以速度v0=10m/s沿
如图所示,滑块A的质量m=0.05kg,与水平地面间的动摩擦因数μ=0.2,用长度不等的细线悬挂的若干个小球,质量均为m=0.05kg,沿x轴排列,且小球与地面间无弹力。滑块A与第1只小球及相邻两小球间距离均为s=2m,细线长分别为L1、L2、L3……(图中只画三只小球,滑块、小球可视为质点)。开始时,滑块A以速度v0=10m/s沿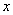 轴正方向运动,设滑块与小球相互碰撞前后速度互相交换,碰撞后小球均恰能在竖直平面内做完整的圆周运动,并再次与滑块碰撞。g取10m/s2,求:
轴正方向运动,设滑块与小球相互碰撞前后速度互相交换,碰撞后小球均恰能在竖直平面内做完整的圆周运动,并再次与滑块碰撞。g取10m/s2,求:
(1)滑块与第1只小球碰撞后瞬间,悬线对小球的拉力为多大?
(2)滑块能与几个小球碰撞?
(3)写出碰撞中第k个小球悬线长Lk的表达式。
 (2010?上海)卡文迪许利用如图所示的扭秤实验装置测量了引力常量G.
(2010?上海)卡文迪许利用如图所示的扭秤实验装置测量了引力常量G.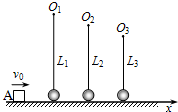 如图所示,滑块A的质量m=0.05kg,与水平地面间的动摩擦因数μ=0.2,用长度不等的细线悬挂的若干个小球,质量均为m=0.05kg,沿x轴排列,且小球与地面间无弹力.滑块A与第1只小球及相邻两小球间距离均为s=2m,细线长分别为L1、L2、L3…(图中只画三只小球,滑块、小球可视为质点).开始时,滑块A以速度v0=10m/s沿x轴正方向运动,设滑块与小球相互碰撞前后速度互相交换,碰撞后小球均恰能在竖直平面内做完整的圆周运动,并再次与滑块碰撞.g取10m/s2,求:
如图所示,滑块A的质量m=0.05kg,与水平地面间的动摩擦因数μ=0.2,用长度不等的细线悬挂的若干个小球,质量均为m=0.05kg,沿x轴排列,且小球与地面间无弹力.滑块A与第1只小球及相邻两小球间距离均为s=2m,细线长分别为L1、L2、L3…(图中只画三只小球,滑块、小球可视为质点).开始时,滑块A以速度v0=10m/s沿x轴正方向运动,设滑块与小球相互碰撞前后速度互相交换,碰撞后小球均恰能在竖直平面内做完整的圆周运动,并再次与滑块碰撞.g取10m/s2,求: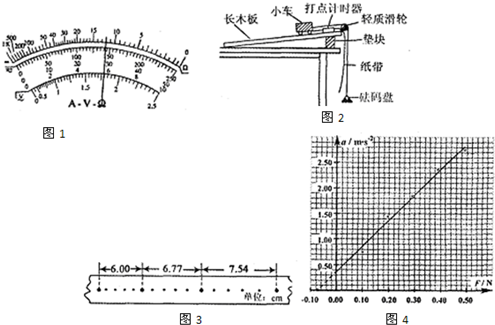
 (2013?海淀区一模)某种角速度计,其结构如图所示.当整个装置绕轴OO′转动时,元件A相对于转轴发生位移并通过滑动变阻器输出电压,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,装置静止时滑片P在变阻器的最左端B端,当系统以角速度ω转动时,则( )
(2013?海淀区一模)某种角速度计,其结构如图所示.当整个装置绕轴OO′转动时,元件A相对于转轴发生位移并通过滑动变阻器输出电压,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,装置静止时滑片P在变阻器的最左端B端,当系统以角速度ω转动时,则( )