Question

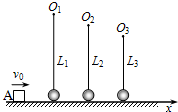如图所示，滑块A的质量m=0.05kg，与水平地面间的动摩擦因数μ=0.2，用长度不等的细线悬挂的若干个小球，质量均为m=0.05kg，沿x轴排列，且小球与地面间无弹力．滑块A与第1只小球及相邻两小球间距离均为s=2m，细线长分别为L₁、L₂、L₃…（图中只画三只小球，滑块、小球可视为质点）．开始时，滑块A以速度v₀=10m/s沿x轴正方向运动，设滑块与小球相互碰撞前后速度互相交换，碰撞后小球均恰能在竖直平面内做完整的圆周运动，并再次与滑块碰撞．g取10m/s²，求：
（1）滑块与第1只小球碰撞后瞬间，悬线对小球的拉力为多大？
（2）滑块能与几个小球碰撞？
（3）写出碰撞中第k个小球悬线长L_k的表达式．

Answer 1

分析：（1）因为小球恰能做圆周运动，求出最高点的临界速度，通过机械能守恒定律求出最低点的速度，根据牛顿第二定律求出悬线对小球的拉力大小．
（2）通过动能定理求出滑块能够向前滑动的距离，结合两球间的距离确定碰撞球的个数．
（3）根据牛顿第二定律求出最高点的临界速度，通过机械能守恒定律求出最低点的速度，结合动能定理求出碰撞中第k个小球悬线长L_k的表达式．

解答：解：（1）设滑块与第1只小球碰前的速度为v₁，由于滑块与小球碰撞后速度交换，即碰撞后小球速度为v₁，滑块静止．
对小球，根据牛顿定律有：F-mg=

m v 2 1

L1

由于小球恰好做完整的圆周运动，设最高点速度为v₁'
根据牛顿定律有：mg=

mv ′ 2 1

L1

根据机械能守恒定律，有：

1

2

m

v

2 1

=

1

2

mv

′

2 1

+2mgL1
由以三各式解得：F=6mg=3N                            
（2）滑块与第1只小球碰撞后互换速度，滑块静止，小球在竖直平面内做圆周运动，当小球回到最低点时，再次与滑块碰撞，小球又静止，滑块向前运动，接着与第2只、第3只等小球发生类似作用．设滑块能与n只小球发生碰撞，与第1、2、3…n只小球碰撞前速度分别为v₁、v₂、v₃…v_n，与第n只小球碰撞后滑行的距离△s后静止，滑行总距离为s₀，根据动能定理有-μmgs=

1

2

m

v

2 1

-

1

2

m

v

2 0

，
-μmgs=

1

2

m

v

2 2

-

1

2

m

v

2 1

，-μmgs=

1

2

m

v

2 3

-

1

2

m

v

2 2

，…-μmgs=

1

2

m

v

2 n

-

1

2

m

v

2 n-1

，-μmg?△s=0-

1

2

m

v

2 n

，
s₀=ns+△s
由以上各式整理得：-μmg?s0=0-

1

2

m

v

2 0

代入数据解得s₀=25m，n=12                                    
（2）设滑块与第k个小球碰撞后，小球速度为v_k，运动到最高点时速度为v_k'，由于小球恰能在竖直平面内完成完整的圆周运动，所以，据牛顿定律有：mg=

mv ′ 2 k

Lk

小球做圆周运动时机械能守恒，根据机械能守恒定律有：

1

2

m

v

2 k

=

1

2

mv

′

2 k

+2mgLk
对滑块，根据动能定理，有：-μmg?ks=

1

2

m

v

2 k

-

1

2

m

v

2 0

由以上三式解得：Lk=

v 2 0 -2kμgs

5g

=(2-0.16k)m
答：（1）滑块与第1只小球碰撞后瞬间，悬线对小球的拉力为3N．
（2）滑块能与12个小球碰撞．
（3）碰撞中第k个小球悬线长L_k的表达式L_k=（2-0.16k）m．

点评：本题综合考查了牛顿第二定律、动能定理、机械能守恒定律等规律，综合性较强，对学生的能力要求较高，需加强这方面的训练．