题目内容
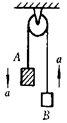
如图所示，A是半径为r的圆形光滑轨道，固定在木板B上，竖直放置；B的左右两侧各有一光滑挡板固定在地面上，使其不能左右运动，小球C静止放在轨道最低点，A，B，C质量相等。现给小球一水平向右的初速度v0，使小球在圆型轨道的内侧做圆周运动，为保证小球能通过轨道的最高点，且不会使B离开地面，初速度v0必须满足（ ）（重力加速度为g）
A．最小值为 | B．最大值为 |
C．最小值为 | D．最大值为 |
CD
解析试题分析：欲使小球刚好能够通过圆型轨道的顶端，则由牛顿第二定律可得，小球在最高点时的速度为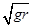
，再由机械能守恒定律可得，小球在C点时的速度为v0=，A不对C是正确的；
如果使B不离开地面，则小球在最高点时对轨道的作用力小于等于2mg，即此进小球的合力为3mg，故再由牛顿第二定律可得此时小球的最大速度为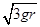
，再由机械能守恒定律可得，小球在C点时的速度最大值为，故D是正确的。
考点：牛顿第二定律，机械能守恒定律。
静止在光滑水平面上的物体，受到恒定的水平拉力作用，由静止开始运动，则该力的作用时间越长，则
| A．物体的速度越大 | B．物体的加速度越大 |
| C．物体的动能越大 | D．在单位时间内对物体所做的功越多 |
某大型游乐场内的新型滑梯可以简化为如图所示的物理模型．一个小朋友从A点开始下滑，滑到C点时速度恰好减为0，整个过程中滑梯保持静止状态．若AB段的动摩擦因数μ1， BC段的动摩擦因数μ2，则该小朋友从斜面顶端A点滑到底端C点的过程中
| A．滑块在AB段的平均速度小于BC段的平均速度 |
| B．AB段的动摩擦因数μ1小于BC段的动摩擦因数μ2 |
| C．地面对滑梯的摩擦力方向始先水平向左后终水平向右 |
| D．地面对滑梯的支持力大小始终等于小朋友和滑梯的总重力大小 |
如图所示，物体A放在一斜面体上，与斜面体一起向右做匀加速直线运动，且与斜面体始终保持相对静止，则
| A．物体A可能受二个力的作用 |
| B．物体A可能受三个力的作用 |
| C．当加速度增加时，物体A受的摩擦力一定增大 |
| D．当加速度增加时，物体A受的摩擦力可能先减小后增大 |
如图所示，长为L的轻杆一端固定一质量为
的小球，另一端安装有固定的转动轴O，杆可在竖直平面内绕轴O无摩擦地转动。若在最低点P处给小球一沿切线方向的初速度
，其中
为重力加速度，不计空气阻力，则（ ）
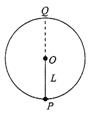
| A．小球不可能到达圆周轨道的最高点Q |
| B．小球能到达最高点Q，但小球在Q点不受轻杆的弹力 |
| C．小球能到达最高点Q，且小球在Q点受到轻杆向上的弹力 |
| D．小球能到达最高点Q，且小球在Q点受到轻杆向下的弹力 |
如图所示，静止在光滑水平面上的物体A，一端靠着处于自然状态的弹簧．现对物体作用一水平恒力，在弹簧被压缩到最短的过程中，物体的速度和加速度的变化情况是 
| A．速度增大，加速度增大 |
| B．速度增大，加速度减小 |
| C．速度先增大后减小，加速度先增大后减小 |
| D．速度先增大后减小，加速度先减小后增大 |
如图所示，带支架的平板小车沿水平面向左做直线运动，小球A用细线悬挂于支架前端，质量为m的物块B始终相对于小车静止地摆放在右端，B与小车平板间的动摩擦因数为μ，若细线偏离竖直方向θ角，则小车对物块B产生的作用力的大小和方向为
| A．mg，竖直向上 | B．mg ，斜向左上方 |
| C．mgtanθ，水平向右 | D．mg ，斜向右上方 |