题目内容
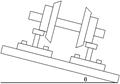
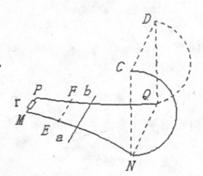
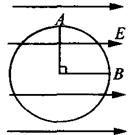
(18分).如图,阻值不计的光滑金属导轨MN和PQ水平放置,其最右端间距d为1m,左端MP,接有阻值r=4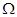 的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
求:(1)杆ab刚进入半圆形导轨时,对导轨的压力:
(2)EF到QN的距离;
(3)磁感应强度B的大小
 的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
求:(1)杆ab刚进入半圆形导轨时,对导轨的压力:
(2)EF到QN的距离;
(3)磁感应强度B的大小
(1)30N(2)4m(3)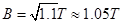
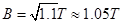
试题分析:(1)设杆ab刚进入半圆形导轨时速度为
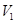 ,到达最高位置CD位置时,速度为
,到达最高位置CD位置时,速度为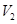 ,由于恰能通过最高点,则:
,由于恰能通过最高点,则: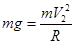
解得
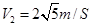
杆ab进入半圆形导轨后,由于轨道绝缘,无感应电流,则根据机械能守恒:
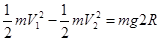
解得

设在最低点时半圆形轨道对杆ab的支持力为N,

则有
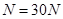
(2)杆ab离开半圆形导轨后做平抛运动,设经时间
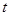 落到水平导轨上
落到水平导轨上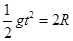
解得
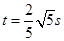
则杆ab与NQ的水平距离
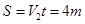
(3)设杆ab做匀减速运动的加速度为a
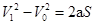
解得

对杆刚要到达NQ位置进行分析
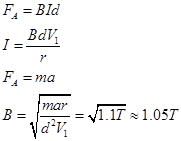
点评:本题通过圆周运动知识分析物体经过最高点时的力学条件,通过机械能守恒定律最后换算处最低处的速度,最后通过支持力与重力合力提供向心力求出未知量。本题还涉及平抛运动,和常见的电磁感应类问题

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
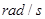 。
。 
 = 。
= 。