题目内容
2.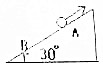 如图所示,在倾角为30°的斜面上,一质量为2kg的物体受到一沿斜面向上大小为4N的F力的作用,从A静止开始向下滑动,加速度大小为2m/s2,当物体运动到B点时,F大小变为14N,方向不变.若AB间距为1m,试求物体在2s内的位移及2s末的速度.
如图所示,在倾角为30°的斜面上,一质量为2kg的物体受到一沿斜面向上大小为4N的F力的作用,从A静止开始向下滑动,加速度大小为2m/s2,当物体运动到B点时,F大小变为14N,方向不变.若AB间距为1m,试求物体在2s内的位移及2s末的速度.
分析 根据牛顿第二定律求出滑动摩擦力的大小,结合速度位移公式求出到达B点的速度,根据牛顿第二定律求出F改为14N时加速度的大小和方向,结合速度时间公式求出速度减为零的时间,从而得出返回匀加速运动的时间,根据牛顿第二定律求出向上的加速度,求出匀加速运动的位移,从而得出2s内的位移.根据速度时间公式求出2s末的速度.
解答 解:根据牛顿第二定律得,${a}_{1}=\frac{mgsin30°-F-f}{m}$,代入数据解得滑动摩擦力f=2N.
根据速度位移公式得,小球到达B点的速度${v}_{B}=\sqrt{2{a}_{1}{x}_{AB}}=\sqrt{2×2×1}$m/s=2m/s,
小球运动到B点的时间${t}_{1}=\frac{{v}_{B}}{{a}_{1}}=\frac{2}{2}s=1s$.
当F改为14N后,小球的加速度${a}_{2}=\frac{F+f-mgsin30°}{m}$=$\frac{14+2-10}{2}m/{s}^{2}=3m/{s}^{2}$,方向沿斜面向上,
则小球速度减为零所需的时间${t}_{2}=\frac{{v}_{B}}{{a}_{2}}=\frac{2}{3}s$,向下做匀减速运动的位移${x}_{2}=\frac{{{v}_{B}}^{2}}{2{a}_{2}}=\frac{4}{6}m=\frac{2}{3}m$,
小球返回做匀加速运动的时间${t}_{3}=2-1-\frac{2}{3}s=\frac{1}{3}s$,小球向上做匀加速直线运动的加速度${a}_{3}=\frac{F-mgsin30°-f}{m}$=$\frac{14-10-2}{2}m/{s}^{2}=1m/{s}^{2}$,
向上做匀加速直线运动的位移${x}_{3}=\frac{1}{2}{a}_{3}{{t}_{3}}^{2}=\frac{1}{2}×1×\frac{1}{9}m=\frac{1}{18}m$,
可知2s内的位移$x={x}_{AB}+{x}_{2}-{x}_{3}=1+\frac{2}{3}-\frac{1}{18}m=1\frac{11}{18}m$≈1.6m.
2s末的速度$v={a}_{3}{t}_{3}=1×\frac{1}{3}m/s=\frac{1}{3}m/s$.
答:物体在2s内的位移为1.6m,2s末的速度为$\frac{1}{3}m/s$.
点评 解决本题的关键理清小球在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,知道加速度是联系力学和运动学的桥梁.

| A. | 质点做匀加速直线运动 | B. | 质点的初速度大小是8m/s | ||
| C. | 质点的加速度大小是2m/s2 | D. | 经过4s,物体速度减为零 |
 如图所示,图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,以下说法正确的是( )
如图所示,图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,以下说法正确的是( )| A. | 带电粒子一定带正电荷 | |
| B. | 可以确定带电粒子在a、b两点的受力方向 | |
| C. | 带电粒子在a点的加速度小于b点的加速度 | |
| D. | 带电粒子在a点的速度小于b点的速度 |
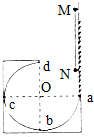 如图所示,固定在水平桌面上的有缺口的方形木块,abcd为半径是R的$\frac{3}{4}$光滑圆弧形轨道,d为圆弧轨道的最高点,M,N是质量均为m的小球(可视为质点)用长2R的轻杆固定,靠在光滑的竖直墙面上,今将N球离a点高度为h处由静止释放,让其自由下落到a处切入轨道内运动,直到N球通d点,不计空气阻力,则( )
如图所示,固定在水平桌面上的有缺口的方形木块,abcd为半径是R的$\frac{3}{4}$光滑圆弧形轨道,d为圆弧轨道的最高点,M,N是质量均为m的小球(可视为质点)用长2R的轻杆固定,靠在光滑的竖直墙面上,今将N球离a点高度为h处由静止释放,让其自由下落到a处切入轨道内运动,直到N球通d点,不计空气阻力,则( )| A. | 只有h大于R,释放后小球N就能通过d点 | |
| B. | 两个小球的速度一定会先增加后减小 | |
| C. | 无论怎样增加h的大小,小球M通过b点时对轨道内侧压力不变 | |
| D. | 无论怎样增加h的大小,小球N通过d点时对轨道内侧压力始终为0 |

| A. | 两个带电粒子的电势能,一个增大一个减小 | |
| B. | 两个带电粒子,一个带正电一个带负电 | |
| C. | a的加速度将减小,b的加速度将增加 | |
| D. | 两个带电粒子的动能都增大 |
| A. | 12cm | B. | 14cm | C. | 13cm | D. | 15cm |
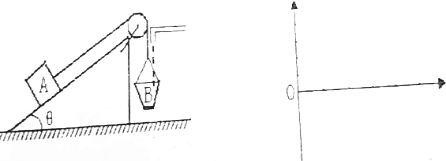
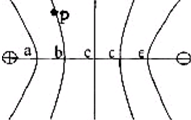 “用描迹法画出电场中平面上的等势线”的实验中,利用电流模拟静电场,所用电源是电压约为6伏的直流电源.实验中同学乙对同学甲已描好的等势线进行验收,他把红表笔定在b处不动,用黑表笔在P点附近移动,电流表的偏转特点是:当电流从红笔流入时指针向右偏,当电流从黑表笔流入时指针向左偏,如果甲的操作是正确的话,则当黑表笔竖直向上移时,指针右偏,当黑表笔从P点沿曲线PB向下移时,指针不偏.(填左偏、右偏或不偏)
“用描迹法画出电场中平面上的等势线”的实验中,利用电流模拟静电场,所用电源是电压约为6伏的直流电源.实验中同学乙对同学甲已描好的等势线进行验收,他把红表笔定在b处不动,用黑表笔在P点附近移动,电流表的偏转特点是:当电流从红笔流入时指针向右偏,当电流从黑表笔流入时指针向左偏,如果甲的操作是正确的话,则当黑表笔竖直向上移时,指针右偏,当黑表笔从P点沿曲线PB向下移时,指针不偏.(填左偏、右偏或不偏)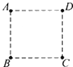 如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=18V、φB=5V、φC=-3V,D点固定一个电子,电子的电势能为-10eV.
如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=18V、φB=5V、φC=-3V,D点固定一个电子,电子的电势能为-10eV.