题目内容
11. 如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=18V、φB=5V、φC=-3V,D点固定一个电子,电子的电势能为-10eV.
如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=18V、φB=5V、φC=-3V,D点固定一个电子,电子的电势能为-10eV.
分析 根据匀强电场中电势差和电场强度的关系 U=Ed,可以知道AB间的电势差等于DC间的电势差,由此求D的电势,再由公式EP=qφ求解电子的电势能.
解答 解:根据匀强电场中电势差和电场强度的关系 U=Ed,可知AB间的电势差等于DC间的电势差,即有:φA-φB=φD-φC,则得D点的电势为:
φD=φA-φB+φC=18-5+(-3)=10V
因此D点固定一个电子,电子的电势能为:
EP=-eφD=-10eV
故答案为:-10eV.
点评 解决本题的关键是掌握公式U=Ed,知道在匀强电场中沿任意方向在相等距离上电势差相等,确定出D点的电势.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
19. 某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
 某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
某电场的电场线的分布如图所示,一个带电粒子只在电场力的作用下由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )| A. | 粒子带负电 | |
| B. | 粒子在M点的加速度大 | |
| C. | 粒子在N点的速度小 | |
| D. | 粒子在M点的电势能比在N点的电势能大 |
6.如表是重庆北站开往成都东站的D5135次动车时刻表,根据表中的信息求,该次动车从重庆北站到大英东站运行过程中的平均速度为多少km/h?(保留一位小数)
| 站次 | 站名 | 到站时间 | 发车时间 | 里程(公里) |
| 1 | 重庆北 | 始发站 | 06:34 | 0 |
| 2 | 合川 | 06:59 | 07:03 | 66 |
| 3 | 潼南 | 07:26 | 07:30 | 115 |
| 4 | 大英东 | 08:04 | 08:07 | 194 |
| 5 | 成都东 | 08:54 | 终点站 | 313 |
16. 一个T型电路如图所示,电路中的电阻分别是R1=10Ω、R2=60Ω、R3=40Ω.另有一测试电源,电动势为80V,内阻忽略不计.则( )
一个T型电路如图所示,电路中的电阻分别是R1=10Ω、R2=60Ω、R3=40Ω.另有一测试电源,电动势为80V,内阻忽略不计.则( )
 一个T型电路如图所示,电路中的电阻分别是R1=10Ω、R2=60Ω、R3=40Ω.另有一测试电源,电动势为80V,内阻忽略不计.则( )
一个T型电路如图所示,电路中的电阻分别是R1=10Ω、R2=60Ω、R3=40Ω.另有一测试电源,电动势为80V,内阻忽略不计.则( )| A. | 当cd端短路时,ab之间的等效电阻是34Ω | |
| B. | 当ab端短路时,cd之间的等效电阻是34Ω | |
| C. | 当ab两端接通测试电源时,cd两端的电压为64V | |
| D. | 当cd两端接通测试电源时,ab两端的电压为64V |
1.下列说法中正确的是( )
| A. | “一江春水向东流”是以水为参考系来描述江水的运动 | |
| B. | 研究一端固定并可其绕转动的木杆的运动时,可把木杆看成质点 | |
| C. | 第7秒初、第8秒末均表示时刻,它们的时间间隔为1秒 | |
| D. | 物体速度为零时,加速度可以不为零 |

 如图所示,在倾角为30°的斜面上,一质量为2kg的物体受到一沿斜面向上大小为4N的F力的作用,从A静止开始向下滑动,加速度大小为2m/s2,当物体运动到B点时,F大小变为14N,方向不变.若AB间距为1m,试求物体在2s内的位移及2s末的速度.
如图所示,在倾角为30°的斜面上,一质量为2kg的物体受到一沿斜面向上大小为4N的F力的作用,从A静止开始向下滑动,加速度大小为2m/s2,当物体运动到B点时,F大小变为14N,方向不变.若AB间距为1m,试求物体在2s内的位移及2s末的速度.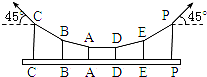 一吊桥由六对钢杆悬吊着,六对钢杆在桥面分列两排,其上端挂在两根钢缆上,如图为其一截面图,已知图中相邻两钢杆间距离均为9m,靠桥面中心的钢杆长度为2m(即AA′=DD′=2m),BB′=EE′,CC′=PP′,又已知两端钢缆与水平成45°.若钢杆、钢缆自重不计,为使每根钢杆承受的负荷相同,试求钢杆BB′和CC′的长度应各为多少?
一吊桥由六对钢杆悬吊着,六对钢杆在桥面分列两排,其上端挂在两根钢缆上,如图为其一截面图,已知图中相邻两钢杆间距离均为9m,靠桥面中心的钢杆长度为2m(即AA′=DD′=2m),BB′=EE′,CC′=PP′,又已知两端钢缆与水平成45°.若钢杆、钢缆自重不计,为使每根钢杆承受的负荷相同,试求钢杆BB′和CC′的长度应各为多少? 在实验室测量两个直流电源的电动势和内电阻,电源甲的电动势大约为4.5V,内阻大约为1.5Ω;电源乙的电动势大约为1.5V,内阻大约为1Ω.由于实验室条件有限,除了导线、开关外,实验室还能提供如下器材:
在实验室测量两个直流电源的电动势和内电阻,电源甲的电动势大约为4.5V,内阻大约为1.5Ω;电源乙的电动势大约为1.5V,内阻大约为1Ω.由于实验室条件有限,除了导线、开关外,实验室还能提供如下器材: