题目内容
如图甲所示,间距为L、足够长的固定光滑平行金属导轨MN、PQ 与水平面成θ角,左端M、P之间连接有电流传感器和阻值为R 的定值电阻.导轨上垂直停放一质量为m、电阻为r的金属杆ab,且与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B 的匀强磁场中.在t=0时刻,用一沿MN方向的力斜向上拉金属杆ab,使之从磁场的左边界由静止开始斜向上做直线运动,电流传感器将通过R 的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g.
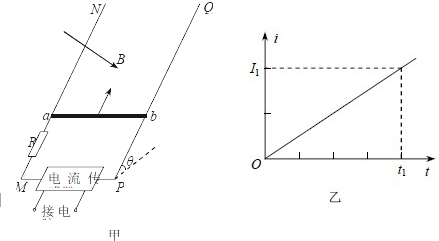 (1)若电流i 随时间t 变化的关系如图乙所示,求t时刻杆ab 的速度υ大小;
(1)若电流i 随时间t 变化的关系如图乙所示,求t时刻杆ab 的速度υ大小;
(2)在(1)问的情况下,请判断杆ab的运动性质,并求t 时刻斜向上拉力的功率P;
(3)若电流i随时间t 变化规律为i=Imsin
t,则在0~1/2T时间内斜向上拉力对杆ab做的功W.
 (1)若电流i 随时间t 变化的关系如图乙所示,求t时刻杆ab 的速度υ大小;
(1)若电流i 随时间t 变化的关系如图乙所示,求t时刻杆ab 的速度υ大小;(2)在(1)问的情况下,请判断杆ab的运动性质,并求t 时刻斜向上拉力的功率P;
(3)若电流i随时间t 变化规律为i=Imsin
| 2π | T |
分析:(1)由乙图看出,i与t成正比,由数学知识可写出i与t的关系式,由e=BLv和闭合电路欧姆定律求出t时刻杆ab的速度v;
(2)根据速度-时间关系式,分析杆ab的运动性质,由速度公式求出杆的加速度大小.杆向上运动的过程中,由牛顿第二定律列式拉力的功率P的大小.
(3)由位移为 x=-Acos
,对位移求导数得到速度的表达式,分析得出杆ab做简谐运动,求电流的有效值,根据焦耳定律求解整个回路产生的热量,再根据功能关系和动能定理求解拉力对杆ab做的功W.
(2)根据速度-时间关系式,分析杆ab的运动性质,由速度公式求出杆的加速度大小.杆向上运动的过程中,由牛顿第二定律列式拉力的功率P的大小.
(3)由位移为 x=-Acos
| 2π |
| T |
解答:解:(1)由乙图可知,t=t1时刻电路中的感应电流为I1,则t时刻,电流为:i=
t…①
杆ab切割磁感线产生的感应电动势为:e=BLv…②
根据闭合电路欧姆定律有:e=i(R+r)…③
由①②③式解得:v=
t…④
(2)由于
是常量,所以杆ab做匀加速直线运动,其加速度大小为:a=
=
…⑤
设t时刻拉力大小为F,根据牛顿第二定律有:F-BiL-mgsinθ=ma…⑥
又 P=Fv…⑦
得:P=
t2+[gsinθ+
]
t…⑧
(3)设位移x=-Acos
t,由导数的物理意义可知,有:v=A?
sin
t…⑨
由BLv=i(R+r)及i=Imsin
t得:v=
sin
t…⑩
可见,杆ab做简谐运动,所以振幅为:A=
…(11)
在0~
T时间内,整个回路产生的焦耳热为:
Q=(
)2(R+r)?
T…(12)
安陪力对杆ab做的功为:W2=-Q…(13)
根据动能定理有:W+W1+W2=
mv2-0…(14)
联立以上四式得:W=
+
(R+r)T…(15)
答:(1)若电流i 随时间t 变化的关系如图乙所示,t时刻杆ab 的速度υ大小为
t;
(2)在(1)问的情况下,杆ab做匀加速直线运动,t时刻斜向上拉力的功率P为
t2+[gsinθ+
]
t;
(3)若电流i随时间t 变化规律为i=Imsin
t,则在0~1/2T时间内斜向上拉力对杆ab做的功W为
+
(R+r)T.
| I1 |
| t1 |
杆ab切割磁感线产生的感应电动势为:e=BLv…②
根据闭合电路欧姆定律有:e=i(R+r)…③
由①②③式解得:v=
| I1(R+r) |
| BLt1 |
(2)由于
| I1(R+r) |
| BLt1 |
| v |
| t |
| I1(R+r) |
| BLt1 |
设t时刻拉力大小为F,根据牛顿第二定律有:F-BiL-mgsinθ=ma…⑥
又 P=Fv…⑦
得:P=
| ||
|
| I1(R+r) |
| BLt1 |
| mI1(R+r) |
| BLt1 |
(3)设位移x=-Acos
| 2π |
| T |
| 2π |
| T |
| 2π |
| T |
由BLv=i(R+r)及i=Imsin
| 2π |
| T |
| Im(R+r) |
| BL |
| 2π |
| T |
可见,杆ab做简谐运动,所以振幅为:A=
| Im(R+r)T |
| 2πBL |
在0~
| 1 |
| 2 |
Q=(
| Im | ||
|
| 1 |
| 2 |
安陪力对杆ab做的功为:W2=-Q…(13)
根据动能定理有:W+W1+W2=
| 1 |
| 2 |
联立以上四式得:W=
| mgIm(R+r)Tsinθ |
| πBL |
| 1 |
| 4 |
| I | 2 m |
答:(1)若电流i 随时间t 变化的关系如图乙所示,t时刻杆ab 的速度υ大小为
| I1(R+r) |
| BLt1 |
(2)在(1)问的情况下,杆ab做匀加速直线运动,t时刻斜向上拉力的功率P为
| ||
|
| I1(R+r) |
| BLt1 |
| mI1(R+r) |
| BLt1 |
(3)若电流i随时间t 变化规律为i=Imsin
| 2π |
| T |
| mgIm(R+r)Tsinθ |
| πBL |
| 1 |
| 4 |
| I | 2 m |
点评:本题的关键首先要运用数学知识写出电流与时间的关系,还考查了牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图甲所示,间距为L=0.3m、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ=30°角,左端M、P之间连接有电流传感器和阻值为R=0.4Ω的定值电阻.导轨上垂直停放一质量为m=0.1kg、电阻为r=0.20Ω的金属杆ab,且与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B=0.50T的匀强磁场中.在t=0时刻,用一与导轨平面平行的外力F斜向上拉金属杆ab,使之从由静止开始沿导轨平面斜向上做直线运动,电流传感器将通过R的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,如图乙所示.电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g=10m/s2.
如图甲所示,间距为L=0.3m、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ=30°角,左端M、P之间连接有电流传感器和阻值为R=0.4Ω的定值电阻.导轨上垂直停放一质量为m=0.1kg、电阻为r=0.20Ω的金属杆ab,且与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B=0.50T的匀强磁场中.在t=0时刻,用一与导轨平面平行的外力F斜向上拉金属杆ab,使之从由静止开始沿导轨平面斜向上做直线运动,电流传感器将通过R的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,如图乙所示.电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g=10m/s2. 如图甲所示,间距为L、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ角,下端M、P之间连接有电流传感器和阻值为R的定值电阻.导轨上垂直停放一质量为m、电阻为r的金属杆ab.ab与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B的匀强磁场中.在t=0时刻,用一沿斜面向上的力向上拉金属杆ab,使之由静止开始斜向上做直线运动,电流传感器将通过R的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,设图乙中的I1和t1为已知数.电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g.
如图甲所示,间距为L、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ角,下端M、P之间连接有电流传感器和阻值为R的定值电阻.导轨上垂直停放一质量为m、电阻为r的金属杆ab.ab与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B的匀强磁场中.在t=0时刻,用一沿斜面向上的力向上拉金属杆ab,使之由静止开始斜向上做直线运动,电流传感器将通过R的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,设图乙中的I1和t1为已知数.电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g.
