题目内容
【题目】如图，质量相同的两小球a，b分别从斜面顶端A和斜面中点B沿水平方向被抛出，恰好均落在斜面底端，不计空气阻力，则以下说法正确的是（ ）
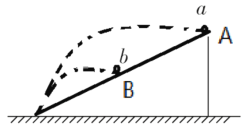
A.小球a，b离开斜面的最大距离之比为2：1
B.小球a，b沿水平方向抛出的初速度之比为2：1
C.小球a，b在空中飞行的时间之比为2：1
D.小球a，b到达斜面底端时速度与水平方向的夹角之比为2：1
【答案】A
【解析】
ABC.因为两球下落的高度之比为1：2，根据
，可知a、b两球运动的时间之比为
因为两球均落在斜面上，则有
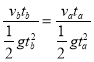
因此初速度之比
当小球平抛过程中，速度方向平行与斜面时，离开斜面的距离为最大，根据运动的分解，将初速度与加速度分解成垂直斜面与平行斜面两方向，设斜面的倾角为α，因此垂直斜面方向的位移为：
（v0sinα）2=2ghcosα
那么离开斜面的最大距离与初速度的平方成正比，即为之比为2：1，故A正确BC错误。
D. 小球落在斜面上时，速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍，因为位移与水平方向的夹角相等，则速度与水平方向的夹角相等，到达斜面底端时速度方向与斜面的夹角也相等，比值为1：1，故D错误。
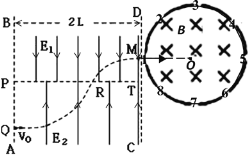
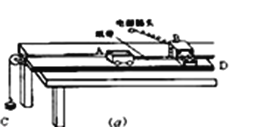
【题目】如图为用拉力传感器和速度传感器探究“加速度与物体受力的关系” 实验装置。用拉力传感器记录小车受到拉力的大小，在长木板上相距L= 48.00 cm的A、B两点各安装一个速度传感器，分别记录小车到达A、B时的速率。
实验主要步骤如下：
①按图装配好装置。
②将拉力传感器固定在小车上
③把细线的一端固定在拉力传感器上，另一端通过定滑轮与钩码相连；
④接通电源后自C点释放小车，小车在细线拉动下运动，记录细线拉力F的大小及小车分别到达A、B时的速率vA、vB；
⑤改变所挂钩码的数量，重复④的操作。
次数 | F | vB2-vA2 | a(m/s2) |
1 | 0.60 | 0.77 | 0.80 |
2 | 1.04 | 1.61 | 1.68 |
3 | 1.42 | 2.34 | |
4 | 2.62 | 4.65 | 4.84 |
6 | 3.00 | 5.49 | 5.72 |
(1)表中记录了实验测得的几组数据，
是两个速度传感器记录速率的平方差，则表格中缺少的中第3次记录的数据加速度a应为_________m/s2（结果保留三位有效数字）；
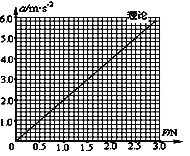
(2)依据表中数据，在坐标纸上作出a～F关系图线_______；
(3)比较实验结果与理论计算得到的关系图线(图中已画出理论图线) ，造成上述偏差的原因是______________________________________________________。
