题目内容
【题目】如图所示,在某一水平地面上的同一直线上,固定一个半径为R的四分之一圆形轨道AB,轨道右侧固定一个倾角为30°的斜面,斜面顶端固定一大小可忽略的轻滑轮,轻滑轮与OB在同一水平高度。一轻绳跨过定滑轮,左端与圆形轨道上质量为m的小圆环相连,右端与斜面上质量为M的物块相连。在圆形轨道底端A点静止释放小圆环,小圆环运动到图中P点时,轻绳与轨道相切,OP与OB夹角为60°;小圆环运动到B点时速度恰好为零。忽略一切摩擦力阻力,小圆环和物块均可视为质点,物块离斜面底端足够远,重力加速度为g,则下列说法正确的是( )
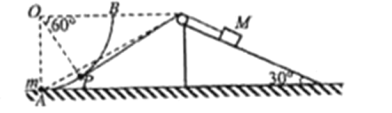
A.小圆环到达B点时的加速度为![]()
B.小圆环到达B点后还能再次回到A点
C.小圆环到达P点时,小圆环和物块的速度之比为2:![]()
D.小圆环和物块的质量之比满足![]()
【答案】B
【解析】
A.小圆环到达B点时受到细线水平向右的拉力和圆弧轨道对圆环的水平向左的支持力,竖直方向受到向下的重力,可知此时小圆环的加速度为g竖直向下,选项A错误;
B.小圆环从A点由静止开始运动,运动到B点时速度恰好为零,且一切摩擦不计,可知小圆环到达B点后还能再次回到A点,选项B正确;
C.小圆环到达P点时,因为轻绳与轨道相切,则此时小圆环和物块的速度相等,选项C错误;
D.当小圆环运动到B点速度恰好为0时,物块M的速度也为0,设圆弧半径为R,从A到B的过程中小圆环上升的高度h=R;物块M沿斜面下滑距离为
![]()
由机械能守恒定律可得
![]()
解得
![]()
选项D错误。
故选B。

练习册系列答案
相关题目