题目内容

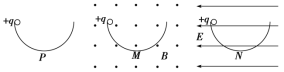
【题目】如图所示，三个完全相同的半圆形光滑轨道竖直放置，分别处在真空、匀强磁场和匀强电场中，轨道两端在同一高度上，三个相同的带正电小球同时从轨道左端最高点由静止开始沿轨道运动，P、M、N分别为轨道的最低点，如图所示，则下列有关判断正确的是(　　)

A. 小球第一次到达轨道最低点的速度关系vp＝vM<vN

B. 小球第一次到达轨道最低点时对轨道的压力关系FP＝FM>FN

C. 小球从开始运动到第一次到达轨道最低点所用的时间关系tP=tM<tN

D. 三个小球到达轨道右端的高度都不相同，但都能回到原来的出发点位置

【答案】C

【解析】

根据动能定理，可得小球到达P、M和N点时的速度；根据牛顿第二定律列式可判断小球第一次到达轨道最低点时对轨道的压力关系；根据到达最低点的速度关系判断时间关系；

根据动能定理，可得小球到达P和M点时的速度： ；在电场中时：，解得： ，可知，A错误；最低点：；；；小球第一次到达轨道最低点时对轨道的压力关系FM>FP >FN；B错误；根据A问答案知道，三球运动到同一高度时，P、M速度相等且大于N点速度，下滑动的路程等于1/4圆弧相等，所以小球从开始运动到第一次到达轨道最低点所用的时间关系tP=tM<tN，C正确；P、M两球机械能守恒，能达到右边等高点，但N球由于电场力做负功不能达到等高点，但三个球都能回到原来的出发点位置，D错误。故选C.

练习册系列答案
相关题目

【题目】如图所示，水平轨道左端与长 的水平传送带相接，传送带逆时针匀速运动的速度。轻弹簧右端固定在光滑水平轨道上，弹簧处于自然状态。现用质量 的小物体(视为质点)将弹簧压缩后由静止释放，到达水平传送带左端 点后，立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动，经圆周最低点 后滑上质量为 的长木板上，竖直半圆轨道的半径，物块与传送带间动摩擦因数，物块与木板间动摩擦因数。取。求：

(1)物块到达点时速度 的大小。

(2)弹簧被压缩时的弹性势能。

(3)若长木块与水平地面间动摩擦因数时，要使小物块恰好不会从长木板上掉下，木板长度的范围是多少(设最大静动摩擦力等于滑动摩擦力)。

【题目】一质量为m的小球在光滑的水平面上以速度做匀速直线运动，在t=0时受到水平方向恒力F作用，速度先减小后增大，其最小值为，由此可以判断（ ）

A. 质点受力F作用后一定做匀速直线运动

B. 质点受力F作用后可能做圆周运动

C. t=0时恒力F与速度方向间的夹角为60°

D. 时，质点速度最小

【题目】如图所示，一辆小车静止在水平地面上，车内固定着一个倾角为60°的光滑斜面OA，光滑挡板OB与水平方向的夹角为θ，挡板OB可绕转轴O在竖直平面内转动。现将重为G的圆球放在斜面与挡板之间。下列说法正确的是（ ）

A. 若θ=60°，球对斜面的压力大小为G

B. 若挡板OB从θ=30°位置沿逆时针方向缓慢转动到θ=90°过程中，则球对斜面的压力逐渐增大

C. 若θ=30°，使小车水平向左做变加速运动，则小车对地面的压力增大

D. 若θ=60°，使小车水平向右做匀加速直线运动，则球对挡板的压力可能为零

【题目】如图所示，光滑水平面MN左端有一固定弹性挡板P(物体与挡板碰撞时无能量损失)，右端N与处于同一高度的水平传送带之间的间隙可忽略，传送带以的速度逆时针匀速转动。MN上放置着三个可视为质点的物体A、B和C，质量分别为mA=4kg、mB=1kg、mC=1kg，开始时，A、B静止，AB间有一个锁定的被压缩的轻质弹簧，弹性势能EP=40J，物体C静止在N点。现解除锁定，A、B被弹开后迅速移走弹簧，B和C相碰后粘在一起。A、B、C三个物体与传送带间的动摩擦因数均为μ=0.2，g=10m/s2。求：

(1)物体A、B被弹开时各自速度的大小；

(2)要使A与BC能在水平面MN上发生相向碰撞，则传送带NQ部分的长度L至少多长；

(3)若传送带NQ部分长度等于(2)问中的最小值，物体A与BC碰撞后结合成整体，此整体从滑上传送带到第一次离开传送带的过程中，系统有多少机械能转化成内能。

【题目】如图甲所示，平面OO′垂直于纸面，其上方有长为h、相距为h的两块平行导体板M、N。两极板间加上如图乙所示的电压，平面OO′的下方是一个与OO′平面平行的匀强磁场，方向垂直纸面向外。在两极板的正中间的正上方有一粒子源，它连续放射出质量为m、带电荷量为+q的粒子，其初速度大小为v0，方向垂直电场及OO′平面。不计粒子重力及空气的阻力，每个粒子在板间运动的极短时间内，可以认为电场强度不变，已知sin37°=0.6，cos37°=0.8。

（1）若要求带电粒子飞出电场时不打在板上，则板间电压U的最大值不能超过多少?

（2）若UMN的最大值取第（1）问求出的最大值，要使所有的粒子通过磁场后都能回到两板间，磁场磁感应强度B的大小及磁场的高度H需满足什么条件?

（3）在满足（2）问的前提下，粒子在磁场中运动的最长时间为多少?

【题目】某同学设计如图所示的电路测电源的电动势和内阻，图中两个电流表相同，定值电阻阻值为R0.

（1）电路中R0的作用为___________。

（2）闭合电键S1之前，先将电阻箱接入电路的阻值调到________（填“最大”或“最小”，闭合电键S1，再闭合电键S2，调节电阻箱的阻值，使电流表A2的指针偏转较大（接近满偏），读出电流值I0，读出这时电阻箱的阻值R1；断开电键S2，调节电阻箱的阻值，使电流表A2的示数再次为I0，读出这时电阻箱的阻值R2，则电流表A1的阻值为_______。

（3）闭合电键S3，依次调大电阻箱的阻值，记录每次调节后电阻箱的阻值R，并记录每次调节后电流表A1的示数I，根据记录的R、I，作出IR-I图象，则图象可能是______.

（4）若根据记录的R、I，作出-R图象，通过对图象的处理，得到图象与纵轴的截距为a，图象的斜率为b，则电源的电动势E=______，电源的内阻r=______。

【题目】2019年1月3日，嫦娥四号探测器成功着陆在月球背面，并通过“鹊桥”中继卫星传回了世界上第一张近距离拍摄月球背面的图片。此次任务实现了人类探测器首次在月球背面软着陆、首次在月球背面通过中继卫星与地球通讯，因而开启了人类探索月球的新篇章。

(1)为了尽可能减小着陆过程中月球对飞船的冲击力，探测器在距月面非常近的距离h处才关闭发动机，此时速度相对月球表面竖直向下，大小为v，然后仅在月球重力作用下竖直下落，接触月面时通过其上的“四条腿”缓冲，平稳地停在月面，缓冲时间为t，如图1所示。已知月球表面附近的重力加速度为g0，探测器质量为m0求：

①探测器与月面接触前瞬间相对月球表面的速度的大小。

②月球对探测器的平均冲击力F的大小。

(2)探测器在月球背面着陆的难度要比在月球正面着陆大很多，其主要的原因在于：由于月球的遮挡，着陆前探测器将无法和地球之间实现通讯。2018年5月，我国发射了一颗名为“鹊桥”的中继卫星，在地球和月球背面的探测器之间搭了一个“桥”，从而有效地解决了通讯的问题。为了实现通讯和节约能量，“鹊桥”的理想位置就是围绕“地一月”系统的一个拉格朗日点运动，如图2所示。所谓“地一月”系统的拉格朗日点是指空间中的某个点，在该点放置一个质量很小的天体，该天体仅在地球和月球的万有引力作用下保持与地球和月球的相对位置不变。

①设地球质量为M，月球质量为m，地球中心和月球中心间的距离为L，月球绕地心运动，图2中所示的拉格朗日点到月球球心的距离为r。推导并写出r与M、m和L之间的关系式。

②地球和太阳组成的“日一地”系统同样存在拉格朗日点，图3为“日-地”系统示意图，请在图中太阳和地球所在直线上用符号 “*”标记出几个可能拉格朗日点的大概位置。

【题目】如图所示，固定的光滑平台上固定有光滑的半圆轨道轨道半径R=0.6m。平台上静止着两个滑块A、B，mA=0.1kg，mB=0.2kg，两滑块间夹有少量炸药，平台右侧有一带挡板的小车，静止在光滑的水平地面上，小车质量为M=0.3kg，车面与平台的台面等高，车面左侧粗糙部分长度为L=0.8m，动摩擦因数为μ=0.2，右侧拴接一轻质弹簧，弹簧自然长度所在范围内车面光滑。点燃炸药后，A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力，滑块B冲上小车。两滑块都可以看作质点，炸药的质量忽略不计，爆炸的时间极短，爆炸后两个物块的速度方向在同一水平直线上，且g=10m/s3，求：

（1）滑块在半圆轨道最低点对轨道的压力。

（2）滑块B滑上小车后的运动过程中弹簧的最大弹性势能。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网