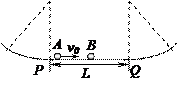题目内容
一根轻且不可伸长细线穿过转轴水平固定的光滑定滑轮,线的两端各系一个质量均为M的同样物体,其中一个物体的侧面爬有质量为m的蟑螂。开始维持两物体不动,并且爬有蟑螂的物体比另一物体高H。放开两物体,当它们并排时,蟑螂垂直于所在物的侧面轻轻跳开,并抓住向上运动的第二个物体。求:
(1)两物体第一次并排时两物体的速度大小;
(2)经过多少时间两物体又并排;
(3)带有蟑螂的第二个物体上升的最大高度。
(1)两物体第一次并排时两物体的速度大小;
(2)经过多少时间两物体又并排;
(3)带有蟑螂的第二个物体上升的最大高度。
(1)
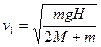 (2)
(2)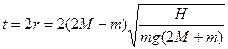 (3)
(3)
(1)两物体第一次并排时蟑螂下降了H/2,两物体速度大小总是相等,可以从能量角度分析。
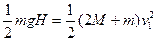 (4分)
(4分)
由此得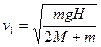 (2分)
(2分)
(2)蟑螂在垂直于下降物体侧面跳开时具有竖直速度,这等于它所离开的物体的速度,这样跳运并不影响此物体速度。但是当蟑螂抓住第二个物体侧面后,系统速度变了。系统的一部分能量转变为内能。可等效处理,根据动量守恒定律求新速度。两物体以速度v1一起运动,蟑螂以同样大小、但相反方向的速度迎面飞去,经这样“碰撞”后速度为
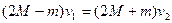 (3分)
(3分)
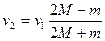 (1分)
(1分)
第一物体以此初速度向下运动的加速度等于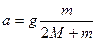 (3分)
(3分)
第一物体运动到最低点所需时间等于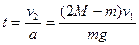 (3分)
(3分)
再经过时间t两物体相齐,则所求时间为
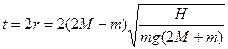 (2分)
(2分)
(3)相对相遇点,带有蟑螂的物体上升高度为
 (4分)
(4分)
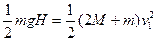 (4分)
(4分)由此得
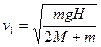 (2分)
(2分)(2)蟑螂在垂直于下降物体侧面跳开时具有竖直速度,这等于它所离开的物体的速度,这样跳运并不影响此物体速度。但是当蟑螂抓住第二个物体侧面后,系统速度变了。系统的一部分能量转变为内能。可等效处理,根据动量守恒定律求新速度。两物体以速度v1一起运动,蟑螂以同样大小、但相反方向的速度迎面飞去,经这样“碰撞”后速度为
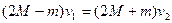 (3分)
(3分)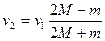 (1分)
(1分)第一物体以此初速度向下运动的加速度等于
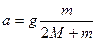 (3分)
(3分)第一物体运动到最低点所需时间等于
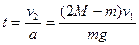 (3分)
(3分)再经过时间t两物体相齐,则所求时间为
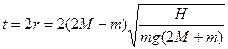 (2分)
(2分)(3)相对相遇点,带有蟑螂的物体上升高度为
 (4分)
(4分)
练习册系列答案
相关题目