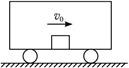
题目内容
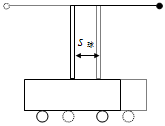
如图所示,长为L的光滑水平轨道PQ与两个曲率半径相同的光滑圆弧轨道相连,圆弧轨道与水平轨道连接处的切线为水平方向,A球以速度v0向右运动,与静止于水平轨道中点处的小球B发生碰撞,碰撞时无机械能损失,已知A、B两球的质量分别为mA,mB,且mA:mB=1:4,小球在圆弧轨道上的运动可认为是简谐运动。(每次碰撞均无机械能损失)试求:
(1)第一次碰撞刚结束时小球A、B各自的速度。
(2)两球第二次碰撞位置距Q点多远?
(3)讨论小球第n次碰撞结束时各自的速度。
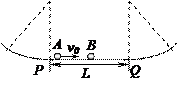
(1)第一次碰撞刚结束时小球A、B各自的速度。
(2)两球第二次碰撞位置距Q点多远?
(3)讨论小球第n次碰撞结束时各自的速度。
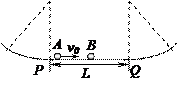
(1)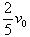 (2)
(2)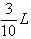 (3)n为奇数时,碰后速度为
(3)n为奇数时,碰后速度为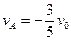
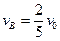
n为偶数时,碰后速度为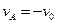
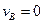
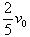 (2)
(2)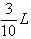 (3)n为奇数时,碰后速度为
(3)n为奇数时,碰后速度为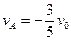
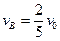
n为偶数时,碰后速度为
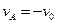
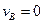
(1)设A、B球第一次碰撞刚结束时的速度分别为v1、v2,取向右为正,由碰撞过程中动量守恒和机械能守恒得: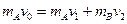 (2分)
(2分)
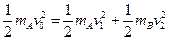 (2分)
(2分)
解得: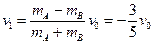
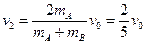 (2分)
(2分)
(2)两球在圆弧轨道上运动的时间均为简谐运动周期的二分之一,时间相等,侧两球在水平轨道上运动的时间也相等。
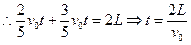 (4分)
(4分)
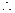 到Q点的距离为
到Q点的距离为 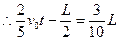 (2分)
(2分)
(3)设第二次碰撞后的A、B球速度分别为v1'、v2',由碰撞中动量守恒和机械能守恒得: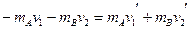 (1分)
(1分)
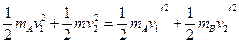 (1分)
(1分)
解得: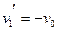
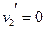 (2分)
(2分)
第三次碰撞前速度与第一次碰撞前相同,因此第一次碰撞后速度与第一次碰撞后速度相同计算可知第四次碰撞又回到中点位置,则第五次碰撞的速度与第一次完全相同
由此可知:n为奇数时,碰后速度为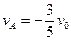
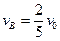
n为偶数时,碰后速度为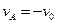
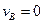 (2分)
(2分)
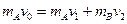 (2分)
(2分)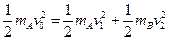 (2分)
(2分)解得:
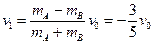
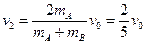 (2分)
(2分)(2)两球在圆弧轨道上运动的时间均为简谐运动周期的二分之一,时间相等,侧两球在水平轨道上运动的时间也相等。
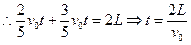 (4分)
(4分)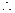 到Q点的距离为
到Q点的距离为 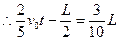 (2分)
(2分)(3)设第二次碰撞后的A、B球速度分别为v1'、v2',由碰撞中动量守恒和机械能守恒得:
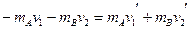 (1分)
(1分)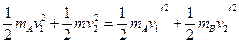 (1分)
(1分)解得:
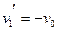
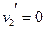 (2分)
(2分)第三次碰撞前速度与第一次碰撞前相同,因此第一次碰撞后速度与第一次碰撞后速度相同计算可知第四次碰撞又回到中点位置,则第五次碰撞的速度与第一次完全相同
由此可知:n为奇数时,碰后速度为
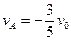
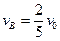
n为偶数时,碰后速度为
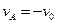
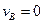 (2分)
(2分)
练习册系列答案
相关题目

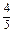 ,求A和B的质量mA与mB之比.
,求A和B的质量mA与mB之比.
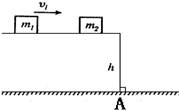
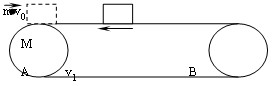
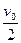 的速度向左运动,则经过多长时间,木块将与后车壁相碰( )
的速度向左运动,则经过多长时间,木块将与后车壁相碰( )