Question

【题目】飞机在500m:的高空以100m/s的速度沿水平航线匀速飞行,飞机在地面上观察者的正上方空投一包裹(取g=10m/s2,不计空气阻力)

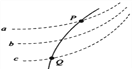
(1)试比较飞行员和地面观察者所见的包裹的运动轨迹;

(2)包裹落地处离地面观察者多远?离飞机的水平距离多大?

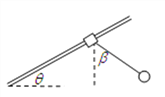
(3)求包裹着地时的速度大小和方向。

Answer 1

【答案】（1）竖直直线、抛物线（2）1000 0 （3） 450

【解析】试题分析：由于惯性，包裹投出后具有和飞机相同的水平速度，地面观察者观察做平抛运动，飞行员一飞机为参考系，做自由落体运动；平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，结合高度求出运动的时间，通过初速度和时间求出水平位移；根据速度时间公式求出竖直分速度，从而根据平行四边形定则求出落地的速度大小和方向。

（1）飞机上的飞行员以正在飞行的飞机为参照物，从飞机上投下去的包裹由于惯性，在水平方向上仍以100m/s的速度沿原来的方向飞行，但由于离开了飞机，在竖直方向上同时进行自由落体运动，所以飞机上的飞行员只是看到包裹在飞机的正下方下落，包裹的轨迹是竖直直线；地面上的观察者是以地面为参照物的，他看见包裹做平抛运动，包裹的轨迹为抛物线。

（2）根据，可得包裹落地的时间：

则包裹落地处离地面观察者的距离为：x=v0t=100×10m=1000m．
因为飞机做匀速直线运动，则包裹落地时离飞机的水平距离为0．

（3）包裹着地时，对地面速度可分解为水平和竖直两个分速度，包裹落地的竖直分速度为：
vy=gt=100m/s，v0=100m/s，

则包裹落地的速度为：

设落地速度与地面夹角为θ：

可得：