Question

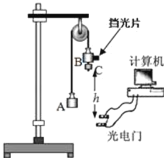
【题目】小明同学用如图所示装置验证机械能守恒定律，轻绳两端跨过转轴光滑的轻滑轮系着质量均为M的重物A和B，将质量为m的小砝码C挂在在物体B上，B下方距离为h处固定一个光电门，物块B装有一宽度很小的挡光片，测得挡光片宽度为d，将系统静止释放，当挡光片通过光电门（固定光电门的装置未画出）时，可通过计算机系统记录挡光时间△t。改变高度差h，重复实验，采集多组h和△t的数据。

(1)若某次记录的挡光时间为△t1，则挡光片到达光电门处时B的速度大小为__。

(2)小明设想，为了确定△t与h的关系，可以分别对△t与h取对数，并以lg△t为纵轴，以lgh为横轴建立坐标系，得到的lg△t﹣lgh图线为一直线，该直线的斜率为__。

(3)若lg△t﹣lgh图线与纵轴交点坐标为c，若机械能守恒，可以得到该地重力加速度g=__。

Answer 1

【答案】

【解析】

(1)[1]根据极短时间内的平均速度等于瞬时速度知，挡光片到达光电门处的速度大小为：

(2)[2]系统重力势能的减小量等于系统动能的增加量，有：

即：

整理可得：

若图线为一直线，则该图线的斜率为

(3)[3]根据得：

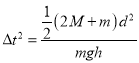
则有：

所以有：

可知纵轴截为：

解得：