题目内容
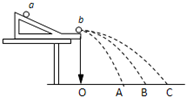
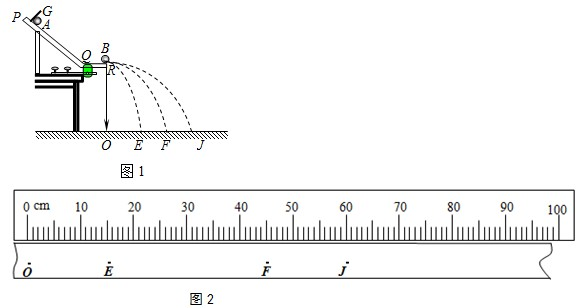
如图是用来验证动量守恒的实验装置,弹性球1用细线悬挂于O点,O点下方桌子的边沿有一竖直立柱.实验时,将球1拉到A点,并使之静止,同时把球2放在立柱上.释放球1,当它摆到悬点正下方时与球2发生对心碰撞.碰后球1向左最远可摆到B点,球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞时动量守恒.现已测出A点离水平桌面的距离为a,B点离水平桌面的距离为b,C点与桌子边沿间的水平距离为c.此外,还需要测量的量是______、______、______、和______.根据测量的数据,该实验中动量守恒的表达式为:______.
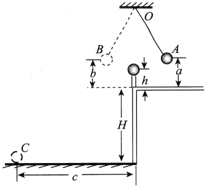

要验证动量守恒,就需要知道碰撞前后的动量,所以要测量12两个小球的质量m1、m2,要通过平抛运动的分位移公式求解碰撞后2球的速度,所以要测量立柱高h,桌面高H;
1小球从A处下摆过程只有重力做功,机械能守恒,根据机械能守恒定律,有
m1g(a-h)=
m1v12
解得:v1=
碰撞后1小球上升到最高点的过程中,机械能守恒,根据机械能守恒定律,有
m1g(b-h)=
m1v22
解得:v2=
碰撞后小球2做平抛运动,
t=
所以2球碰后速度v3=
=
所以该实验中动量守恒的表达式为:m1v1=m2v3+m1v2
带入数据得:2m1
=2m1
+m2
故答案为:弹性球1、2的质量m1、m2;立柱高h;桌面高H;2m1
=2m1
+m2
1小球从A处下摆过程只有重力做功,机械能守恒,根据机械能守恒定律,有
m1g(a-h)=
| 1 |
| 2 |
解得:v1=
| 2g(a-h) |
碰撞后1小球上升到最高点的过程中,机械能守恒,根据机械能守恒定律,有
m1g(b-h)=
| 1 |
| 2 |
解得:v2=
| 2g(b-h) |
碰撞后小球2做平抛运动,
t=
|
所以2球碰后速度v3=
| x |
| t |
| c | ||||
|
所以该实验中动量守恒的表达式为:m1v1=m2v3+m1v2
带入数据得:2m1
| a-h |
| b-h |
| c | ||
|
故答案为:弹性球1、2的质量m1、m2;立柱高h;桌面高H;2m1
| a-h |
| b-h |
| c | ||
|

练习册系列答案
相关题目