��Ŀ����
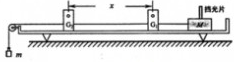
ijͬѧ����ͼ1��ʾװ��̽��A��B��������ײ�ж����Ƿ��غ㣮��ͬѧ����ƽ���˶�����������ײǰ����ٶȣ�ʵ��װ�ú;����������£�ͼ��PQ��б�ۣ�QRΪˮƽ�ۣ�ʵ��ʱ��ʹA���б����ijһ�̶�λ��G�ɾ�ֹ��ʼ���£��䵽λ��ˮƽ����ļ�¼ֽ�ϣ����ºۼ����ظ���������10�Σ��õ�10�����ۼ����ٰ�B�����ˮƽ���Ͽ�����ĩ�˵ĵط�����A���Դ�λ��G�ɾ�ֹ��ʼ���£���B����ײ��A��B��ֱ��ڼ�¼ֽ�����¸��Ե����ۼ����ظ����ֲ���10�Σ�������ʵ����A��B��С������ƽ��λ�ã�ͼ��O����ˮƽ��ĩ��R�ڼ�¼ֽ�ϵĴ�ֱͶӰ�㣮�����׳�ˮƽ���ã���ƽ����G��R��O���ڵ���ֱƽ�棬�׳ߵ������O����룮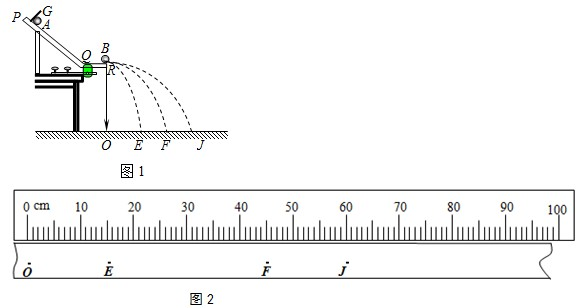
��1��Ϊ��ʹ������ײΪһά��ײ����ѡ�����ֱ����ϵΪ��A���ֱ��______B���ֱ���������ڡ��������ڡ���С�ڡ�����Ϊ��Сʵ������������ײ��ʹA��������ѡ�õ���С��������ϵӦΪmA______mB��ѡ�С�ڡ��������ڡ����ڡ�����
��2��������ѡ���У���Щ�DZ���ʵ�������еIJ�������______����ѡ��ţ���
A��ˮƽ����δ��B��ʱ������A�����λ�õ�O��ľ���
B��A����B����ײ����A����B�����λ�õ�O��ľ���
C��A���B���ڿռ���е�ʱ��
D������G�������ˮƽ����ĸ߶�
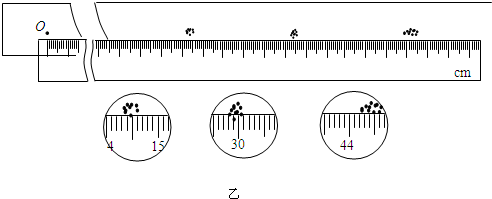
��3����֪mA��mB=2��1��E��F��J��ʵ����С������ƽ��λ�ã�������ݸ�ͬѧʵ������ѡС���ʵ��ļ�¼ֽ�жϣ�A��û����ײB��ʱ�������______�㣨��E��F��J���������ѡ���A����B����ײ��A��������______�㣨��E��F��J���������ѡ���
��ͬѧͨ��ʵ������˵����ʵ����A��B������ײ�ж����غ㣬
������ͼ2�е���ĸд����ͬѧ�ж϶����غ�ı���ʽ��______��

��1��Ϊ��ʹ������ײΪһά��ײ����ѡ�����ֱ����ϵΪ��A���ֱ��______B���ֱ���������ڡ��������ڡ���С�ڡ�����Ϊ��Сʵ������������ײ��ʹA��������ѡ�õ���С��������ϵӦΪmA______mB��ѡ�С�ڡ��������ڡ����ڡ�����
��2��������ѡ���У���Щ�DZ���ʵ�������еIJ�������______����ѡ��ţ���
A��ˮƽ����δ��B��ʱ������A�����λ�õ�O��ľ���
B��A����B����ײ����A����B�����λ�õ�O��ľ���
C��A���B���ڿռ���е�ʱ��
D������G�������ˮƽ����ĸ߶�
��3����֪mA��mB=2��1��E��F��J��ʵ����С������ƽ��λ�ã�������ݸ�ͬѧʵ������ѡС���ʵ��ļ�¼ֽ�жϣ�A��û����ײB��ʱ�������______�㣨��E��F��J���������ѡ���A����B����ײ��A��������______�㣨��E��F��J���������ѡ���
��ͬѧͨ��ʵ������˵����ʵ����A��B������ײ�ж����غ㣬
������ͼ2�е���ĸд����ͬѧ�ж϶����غ�ı���ʽ��______��
��1��Ϊ��ʹ������ײΪһά��ײ����ʵ�ֶ�����ײ����A���ֱ������B���ֱ����
��С����ײ������ˮƽ�������غ㶨�ɣ�����mAv0=mAv1+mBv2
����ײ�����ж����غ㣬����
mAv02=
mAv12+
mBv22
�������v1=
v0��Ҫ��������С����ٶ�v1��0����mA-mB��0����mA��mB��
��2�����ݶ����غ��У�mAv0=mAv1+mBv2����Ϊv0=
��v1=
��v2=
����Ϊʱ����ͬ��������ˮƽλ�ƴ����ٶȣ�������Ҫ����ˮƽ����δ��B��ʱ��A�����λ�õ�O��ľ��룬A����B����ײ��A����B�����λ�õ�O��ľ��룮��A��B��ȷ��
��ѡ��AB��
��3��A����B������A����ٶȼ�С����֪A��û����ײB��ʱ�������F�㣬A����B����ײ��A��������E�㣮��ˮƽλ�ƴ����ٶȣ������غ�ı���ʽΪ��
mAOF=mAOE+mBOJ��
�ʴ�Ϊ����1�����ڣ����� ��2��AB�� ��3��F��E��mAOF=mAOE+mBOJ
��С����ײ������ˮƽ�������غ㶨�ɣ�����mAv0=mAv1+mBv2
����ײ�����ж����غ㣬����
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�������v1=
| mA-mB |
| mA+mB |
��2�����ݶ����غ��У�mAv0=mAv1+mBv2����Ϊv0=
| x1 |
| t |
| x2 |
| t |
| x3 |
| t |
��ѡ��AB��
��3��A����B������A����ٶȼ�С����֪A��û����ײB��ʱ�������F�㣬A����B����ײ��A��������E�㣮��ˮƽλ�ƴ����ٶȣ������غ�ı���ʽΪ��
mAOF=mAOE+mBOJ��
�ʴ�Ϊ����1�����ڣ����� ��2��AB�� ��3��F��E��mAOF=mAOE+mBOJ

��ϰ��ϵ�д�
�����Ŀ