��Ŀ����
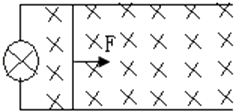
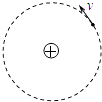
����Ŀ����ͼ��ʾ����ˮƽ���37�����б���AC�����ӳ�����D�����Բ������У�����뾶R=1m��ȫ�����Ϊ��Ե�����Ƴ���λ����ֱ���ڣ������ռ����ˮƽ�������ǿ�糡��MN���Ҳ���ڴ�ֱ��ֽ���������ǿ�ų���C����MN�߽��ϣ���һ����Ϊ0.4kg�Ĵ���С���ع��AC�»�����C��ʱ�ٶ�Ϊv0= ![]() m/s��������ֱ��CD�˶���D�������Բ���������ʱ������ʧ����ǡ����ͨ��F�㣬��F���ٶ�vf=4m/s�������ƿ���������g=10m/s2 �� cos37��=0.8����
m/s��������ֱ��CD�˶���D�������Բ���������ʱ������ʧ����ǡ����ͨ��F�㣬��F���ٶ�vf=4m/s�������ƿ���������g=10m/s2 �� cos37��=0.8����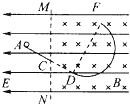
��1��С������ֵ�ɣ�
��2��С���ڰ�Բ������ֿ˷�Ħ���������Ĺ���
��3��С���F��ɳ�ʱ�ų�ͬʱ��ʧ��С���뿪F�����˶��켣��ֱ��AC�����ӳ��ߣ��Ľ���ΪG��G��δ���������G�㵽D��ľ��룮
���𰸡�
��1���⣺С���ܵ��������糡���������������ã����С������磬�糡��ˮƽ���ң���������б�����·���������ֱ���£�С���ܵ��ĺ���������Ϊ�㣬Ҳ���������ٶȷ�����ͬһֱ���ϣ�С������ֱ���˶�����С������磮
��С�������ɣ�
��2���⣺С����CD��������ֱ���˶�������C����ٶ���D����ٶ���ȣ�����v0= ![]() m/s��
m/s��
�糡���������ĺ�����F= ![]() =5N��
=5N��
��D��F���̣���С��
���˶������ɵã���Wf��F2R= ![]() mvF2��
mvF2�� ![]() mv02��
mv02��
�������ݽ�ã�Wf=27.6J��
��С���ڰ�Բ������ֿ˷�Ħ���������Ĺ�27.6J��
��3���⣺��CD�Σ���������糡������ΪF��
��F=qvB��������糡��������F= ![]() =
= ![]() =5N��
=5N��
С���뿪F������ƽ���˶������ٶȣ�a= ![]() ��
��
2R= ![]() at2���������ݽ�ã�t=0.4
at2���������ݽ�ã�t=0.4 ![]() s��
s��
s=vFt=4��0.4 ![]() ��2.26m��
��2.26m��
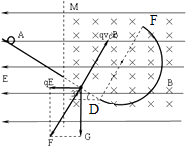
��G�㵽D��ľ���Ϊ2.26m��
������������������ֻ�е糡����б��������ȼ����˶�����糡��ų���ϵij���������ֱ���˶�������������������糡������ƽ��״̬�������ذ�Բ����˶��պ��ܴﵽD�㣬����D������ƽ���˶�����ʱ���ܵ��ĺ����������ٶ����ֱ������ɵ糡����糡ǿ�ȷ����ȷ��С���������ԣ�ͬʱ����ƽ���˶����ɿɵ�С��ֱ���ٶȷ����Ϸ�����λ�ƣ��Ӷ�����˶���ʱ�䣬����ȷ�����ٶȷ�����˶���λ�ƣ�С���ڰ�Բ��������˶������ɵÿ˷�Ħ�����������٣�