题目内容
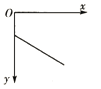
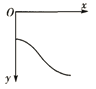
【题目】如图所示,半径![]() 的大圆环竖直固定放置,O点是大圆环的圆心,O'点是O点正上方一个固定点。一根长为L=5 m的轻绳一端固定在O'点,另一端系一质量m=1 kg的小球,将轻绳拉至水平并将小球由静止释放,小球运动到最低点O时,轻绳刚好被拉断。已知重力加速度g=10 m/s2,求:
的大圆环竖直固定放置,O点是大圆环的圆心,O'点是O点正上方一个固定点。一根长为L=5 m的轻绳一端固定在O'点,另一端系一质量m=1 kg的小球,将轻绳拉至水平并将小球由静止释放,小球运动到最低点O时,轻绳刚好被拉断。已知重力加速度g=10 m/s2,求:

(1)轻绳所能承受的最大拉力;
(2)小球落至大圆环上时的动能。
【答案】30N 100J
【解析】试题分析:轻绳被拉断前瞬间所承受的拉力最大.先根据机械能守恒定律求出小球运动到最低点的速度,结合牛顿第二定律求出绳子的最大拉力;绳子断裂后,小球做平抛运动,结合平抛运动的规律,抓住竖直位移和水平位移的关系求出运动的时间,再求出小球落到大圆环上的速度,从而求出动能。
(1)小球由静止运动到O点的过程中机械能守恒,有:![]()
小球在最低点O时,由牛顿第二定律有![]()
解得:Fm=30 N
由牛顿第三定律可知,轻绳所能承受的最大拉力为30 N。
(2)绳被拉断后,小球做平抛运动,设平抛运动的时间为t,
在水平方向:![]()
在竖直方向:![]()
位移间关系为:![]()
联立并代入数据得:t=1s
小球落在大圆环上时速度为:![]()
小球的动能为:![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目