题目内容
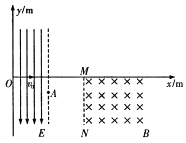
【题目】如图所示,在O≤x≤2m的区域内存在着沿![]() 轴方向的匀强电场E,E在
轴方向的匀强电场E,E在![]() 轴方向区域足够大.有一个比荷为
轴方向区域足够大.有一个比荷为![]() 带正电粒子(粒子重力不计)从O点出发,以
带正电粒子(粒子重力不计)从O点出发,以![]() 的初速度字沿
的初速度字沿![]() 轴正方向射入电场,经过点A(2,-0.75)离开电场.在第四象限垂直于
轴正方向射入电场,经过点A(2,-0.75)离开电场.在第四象限垂直于![]() 轴的边界MN右侧的区域有磁感应强度为B的匀强磁场,M点的坐标为(4.2,0).粒子进入磁场后,又穿过边界MN离开磁场.求:
轴的边界MN右侧的区域有磁感应强度为B的匀强磁场,M点的坐标为(4.2,0).粒子进入磁场后,又穿过边界MN离开磁场.求:
(1)电场强度E的大小;
(2)满足条件的磁感应强度B的最小值;
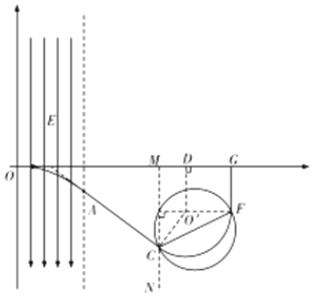
(3)若磁感应强度保持(2)中的最小值,将磁场区域改成圆形,为了使粒子能垂直击中![]() 轴上点G
轴上点G![]() ,求磁场区域的最小面积.
,求磁场区域的最小面积.
【答案】(1)![]() ;(2)1T;(3)
;(2)1T;(3)![]() m2
m2
【解析】
(1)由牛顿第二定律:F=qE=ma
由类平抛运动
X=v0t
![]()
解得:![]() ;
;
(2)由平抛运动可得:
A点的速度![]() ,方向与x轴成
,方向与x轴成![]()

由几何关系可得,入射点![]()
R最大时,![]()
解得:![]()
由![]()
解得此时B为最小,B=1T;
(3)由几何关系可知,粒子仍从C点射放磁场,并
由F点离开磁场,![]() 垂直x轴,且
垂直x轴,且![]()
运动轨迹只有CF在磁场中,由几何关系可得:
![]()
由题意可知最小磁场区域即为以![]() 为直径的圆
为直径的圆
所以![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目