题目内容
12. “儿童蹦极”中,栓在腰间左右两侧的是弹性极好的橡皮绳.如图所示,质量为的m小明静止悬挂时两橡皮绳的拉力大小均恰为mg,若此时小明左侧橡皮绳在腰间断裂,则小明此时的加速度( )
“儿童蹦极”中,栓在腰间左右两侧的是弹性极好的橡皮绳.如图所示,质量为的m小明静止悬挂时两橡皮绳的拉力大小均恰为mg,若此时小明左侧橡皮绳在腰间断裂,则小明此时的加速度( )| A. | 为零 | |
| B. | 大小为g,方向沿原断裂绳的方向斜向下 | |
| C. | 大小为g,方向沿未断裂绳的方向斜向上 | |
| D. | 大小为g,方向竖直向下 |
分析 小明静止时受到重力和两根橡皮条的拉力,处于平衡状态,三力平衡时,三个力中任意两个力的合力与第三个力等值、反向、共线;撤去一个力后,其余两个力未变,故合力与撤去的力等值、反向、共线,求出合力后根据牛顿第二定律求解加速度.
解答 解:小明静止时受到重力和两根橡皮条的拉力,处于平衡状态,由于T1=T2=mg,故两个拉力的合力一定在角平分线上,且在竖直线上,故两个拉力的夹角为120°,当右侧橡皮条拉力变为零时,左侧橡皮条拉力不变,重力也不变;由于三力平衡时,三个力中任意两个力的合力与第三个力等值、反向、共线,故左侧橡皮条拉力与重力的合力与右侧橡皮条断开前的弹力反方向,大小等于mg,故加速度为g,沿原断裂绳的方向斜向下;
故选:B.
点评 本题关键是对小明受力分析后,根据三力平衡时,三个力中任意两个力的合力与第三个力等值、反向、共线来确定撤去一个力后的合力,再根据牛顿第二定律求解加速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图所示,长为L的轻绳悬挂一个质量为m的小球,开始时绳竖直,小球与一个倾角θ=45°的静止三角形物块刚好接触,现在用水平恒力F向左推动三角形物块,直至轻绳与斜面平行,此时小球的速度大小为v,已知重力加速度为g,不计所有的摩擦,则在此过程中( )
如图所示,长为L的轻绳悬挂一个质量为m的小球,开始时绳竖直,小球与一个倾角θ=45°的静止三角形物块刚好接触,现在用水平恒力F向左推动三角形物块,直至轻绳与斜面平行,此时小球的速度大小为v,已知重力加速度为g,不计所有的摩擦,则在此过程中( )
 如图所示,长为L的轻绳悬挂一个质量为m的小球,开始时绳竖直,小球与一个倾角θ=45°的静止三角形物块刚好接触,现在用水平恒力F向左推动三角形物块,直至轻绳与斜面平行,此时小球的速度大小为v,已知重力加速度为g,不计所有的摩擦,则在此过程中( )
如图所示,长为L的轻绳悬挂一个质量为m的小球,开始时绳竖直,小球与一个倾角θ=45°的静止三角形物块刚好接触,现在用水平恒力F向左推动三角形物块,直至轻绳与斜面平行,此时小球的速度大小为v,已知重力加速度为g,不计所有的摩擦,则在此过程中( )| A. | 斜面对小球做的功等于小球增加的动能 | |
| B. | 推力F做的功等于小球增加的机械能 | |
| C. | 小球的机械能守恒 | |
| D. | 推力F做的功为FL |
3.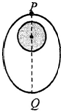 某些军事卫星需要在特定地区上空待较长时间,所以运行轨道会设计为椭圆.如题图所示,JP为轨道近地点,Q为远地点,卫星仅受引力作用,则有( )
某些军事卫星需要在特定地区上空待较长时间,所以运行轨道会设计为椭圆.如题图所示,JP为轨道近地点,Q为远地点,卫星仅受引力作用,则有( )
 某些军事卫星需要在特定地区上空待较长时间,所以运行轨道会设计为椭圆.如题图所示,JP为轨道近地点,Q为远地点,卫星仅受引力作用,则有( )
某些军事卫星需要在特定地区上空待较长时间,所以运行轨道会设计为椭圆.如题图所示,JP为轨道近地点,Q为远地点,卫星仅受引力作用,则有( )| A. | 从P点运行到Q点过程,速度逐渐增大 | |
| B. | 从P点运行到Q点过程,加速度逐渐减小 | |
| C. | 运行过程中卫星的动能与引力势能之和不变 | |
| D. | 运行周期小于近地轨道卫星周期 |
7.下列说法中正确的是( )(填正答案的标号)
| A. | 太阳辐射的能量主要来自太阳内部的核聚变反应 | |
| B. | 在核反应中,反应前后质量数相同,电荷数相同 | |
| C. | 元素衰变中放出的β射线是原子核中质子与中子结合而成的 | |
| D. | 在核反应式${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+X中,X表示质子 | |
| E. | 原子核的比结合能越大,表明组成原子核的核子数越多 |
4. 如图,平行倾斜的光滑导轨宽度为0.2m,上端连接图示的电源E,当导体棒ab垂直放在导轨上时,有2.5A电流的通过棒,已知棒的质量为0.1kg,轨道倾角θ=30°,g=10m/s2.则下列说法正确的是( )
如图,平行倾斜的光滑导轨宽度为0.2m,上端连接图示的电源E,当导体棒ab垂直放在导轨上时,有2.5A电流的通过棒,已知棒的质量为0.1kg,轨道倾角θ=30°,g=10m/s2.则下列说法正确的是( )
 如图,平行倾斜的光滑导轨宽度为0.2m,上端连接图示的电源E,当导体棒ab垂直放在导轨上时,有2.5A电流的通过棒,已知棒的质量为0.1kg,轨道倾角θ=30°,g=10m/s2.则下列说法正确的是( )
如图,平行倾斜的光滑导轨宽度为0.2m,上端连接图示的电源E,当导体棒ab垂直放在导轨上时,有2.5A电流的通过棒,已知棒的质量为0.1kg,轨道倾角θ=30°,g=10m/s2.则下列说法正确的是( )| A. | 如果加上磁感应强度B=2 T的匀强磁场,则棒所受安培力F一定是1 N | |
| B. | 如果发现棒所受的安培力F=0,则一定没有加磁场 | |
| C. | 如果所加的匀强磁场的B=0.5T,要使棒静止,则滑动变阻器R的滑片必须上滑 | |
| D. | 如果所加匀强磁场的B=2T,则棒不能静止在导轨上 |
1. 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计,线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计,线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计,线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计,线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )| A. | 图示位置穿过线框的磁通量为零 | |
| B. | 线框中产生交变电压的有效值为500V | |
| C. | 变压器原、副线圈匝数之比为25:11 | |
| D. | 允许变压器输出的最大功率为5000W |
 如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接,一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2,求:
如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接,一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2,求:
 如图所示,质量为m的小球(视为质点),用轻软绳系在固定的边长为a的正方形截面木柱的顶角A处(木柱水平,图中斜线部分为其竖直横截面),软绳长为4a,软绳所能承受的最大拉力T=9mg,软绳开始时拉直并处于水平状态,问此时应以多大的初速度竖直下抛小球,才能使绳绕在木柱上且个小段均做圆周运动最后击中A点?
如图所示,质量为m的小球(视为质点),用轻软绳系在固定的边长为a的正方形截面木柱的顶角A处(木柱水平,图中斜线部分为其竖直横截面),软绳长为4a,软绳所能承受的最大拉力T=9mg,软绳开始时拉直并处于水平状态,问此时应以多大的初速度竖直下抛小球,才能使绳绕在木柱上且个小段均做圆周运动最后击中A点?