题目内容
2. 如图所示,质量为m的小球(视为质点),用轻软绳系在固定的边长为a的正方形截面木柱的顶角A处(木柱水平,图中斜线部分为其竖直横截面),软绳长为4a,软绳所能承受的最大拉力T=9mg,软绳开始时拉直并处于水平状态,问此时应以多大的初速度竖直下抛小球,才能使绳绕在木柱上且个小段均做圆周运动最后击中A点?
如图所示,质量为m的小球(视为质点),用轻软绳系在固定的边长为a的正方形截面木柱的顶角A处(木柱水平,图中斜线部分为其竖直横截面),软绳长为4a,软绳所能承受的最大拉力T=9mg,软绳开始时拉直并处于水平状态,问此时应以多大的初速度竖直下抛小球,才能使绳绕在木柱上且个小段均做圆周运动最后击中A点?
分析 小球的运动过程中满足机械能守恒,掌握小球在竖直面内圆周运动能通过最高点的临界条件v$≥\sqrt{gR}$进行求解.
解答 解:在最低点,对小球应用牛顿第二定律得:
$T-mg=m\frac{{v}_{1}^{2}}{{R}_{1}}$
由上式可知,小球圆周运动半径越小,绳子越容易断,故小球在最低点时,应取以B为圆心即R1=3a,并保障绳子不被拉断有:
9mg-mg=$m\frac{{v}_{1}^{2}}{3a}$
解得小球在最低点的最大速度为:${v}_{1}=\sqrt{24ga}$
设开始下抛的初速度为v0,从开始至最低点应用动能定理得:
$mg×4a=\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{0}^{2}$
代入${v}_{1}=\sqrt{24ga}$
可解得:${v}_{0}=4\sqrt{ga}$
若小球恰好能通过最高点,则在最高点处有:mg=$m\frac{{v}_{2}^{2}}{{R}_{2}}$
由该式可见R2最大时,通过最高点所需v2越大,故应取C点为圆心,即R2=2a才能完成圆周运动.
mg=$m\frac{{v}_{2}^{2}}{2a}$
解得:${v}_{2}=\sqrt{2ga}$
从开始至最高点时应用动能定理有:
$-mga=\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{0}^{2}$
代入${v}_{2}=\sqrt{2ga}$可解得:${v}_{0}=3\sqrt{ga}$
综上可知,使绳绕在木柱上且个小段均做圆周运动最后击中A点小球竖直下抛的速度满足:$3\sqrt{ga}≤{v}_{0}≤4\sqrt{ga}$
答:此时应以$3\sqrt{ga}≤{v}_{0}≤4\sqrt{ga}$的初速度竖直下抛小球,才能使绳绕在木柱上且个小段均做圆周运动最后击中A点.
点评 解决本题的关键是抓住小球在竖直面内圆周运动的通过最高点的临界条件和向心力大小的判定,抓住条件展开讨论是解决问题的关键.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 “儿童蹦极”中,栓在腰间左右两侧的是弹性极好的橡皮绳.如图所示,质量为的m小明静止悬挂时两橡皮绳的拉力大小均恰为mg,若此时小明左侧橡皮绳在腰间断裂,则小明此时的加速度( )
“儿童蹦极”中,栓在腰间左右两侧的是弹性极好的橡皮绳.如图所示,质量为的m小明静止悬挂时两橡皮绳的拉力大小均恰为mg,若此时小明左侧橡皮绳在腰间断裂,则小明此时的加速度( )| A. | 为零 | |
| B. | 大小为g,方向沿原断裂绳的方向斜向下 | |
| C. | 大小为g,方向沿未断裂绳的方向斜向上 | |
| D. | 大小为g,方向竖直向下 |
| A. | 做曲线运动的物体,所受的合力可以为恒力 | |
| B. | 物体运动的速率不变,所受的合力一定为0 | |
| C. | 物体所受合力方向与运动方向相反,该物体一定做直线运动 | |
| D. | 物体做匀速圆周运动时,所受的合力一定指向圆心 |
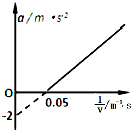 一辆汽车在平直的公路上运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示,若已知汽车的质量为2×103kg,则根据图象所给的信息,可求出( )
一辆汽车在平直的公路上运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示,若已知汽车的质量为2×103kg,则根据图象所给的信息,可求出( )| A. | 汽车的功率为8×104W | |
| B. | 汽车行驶的最大速度为40m/s | |
| C. | 汽车所受到的阻力为2000N | |
| D. | 汽车运动到最大速度所需的时间为20s |
| A. | 加速度大小为2m/s2 | B. | 第1s内的位移为8m | ||
| C. | 第2s末的速度为16m/s | D. | 前2s内的平均速度为8m/s |
 如图甲所示,MN、PQ是固定在绝缘水平面上的两平行金属导轨,两导体棒ab、cd垂直于导轨放置且与两导轨接触良好,两导体棒中间有一根绝缘轻质细线相连,整个装置放在垂直于水平面的变化磁场中,磁场的磁感应强度变化情况如图乙所示,则关于回路中的感应电流i,绝缘细线中的张力F在从零到t0时间内的变化情况,正确的是( )
如图甲所示,MN、PQ是固定在绝缘水平面上的两平行金属导轨,两导体棒ab、cd垂直于导轨放置且与两导轨接触良好,两导体棒中间有一根绝缘轻质细线相连,整个装置放在垂直于水平面的变化磁场中,磁场的磁感应强度变化情况如图乙所示,则关于回路中的感应电流i,绝缘细线中的张力F在从零到t0时间内的变化情况,正确的是( )| A. | i逐渐减小到零 | B. | i始终保持不变 | C. | F逐渐减小到零 | D. | F始终保持不变 |

| A. | 质点运动的频率是3Hz | B. | 质点振动的频率是4Hz | ||
| C. | 在10s内,质点经过的路程是20cm | D. | 第4s末,质点的速度是零 |
 如图所示,小物体在竖直平面内做圆周运动,若突然松手或是绳子断了,物体将沿切线方向飞出而做远离圆心的运动,产生该现象的原因是:外力不足以提供向心力.
如图所示,小物体在竖直平面内做圆周运动,若突然松手或是绳子断了,物体将沿切线方向飞出而做远离圆心的运动,产生该现象的原因是:外力不足以提供向心力. 如图所示,质量为2Kg的物体置于水平面上,在水平拉力F作用下从静止开始沿水平面做匀加速直线运动,求:
如图所示,质量为2Kg的物体置于水平面上,在水平拉力F作用下从静止开始沿水平面做匀加速直线运动,求: