题目内容
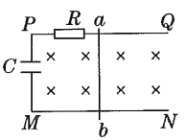
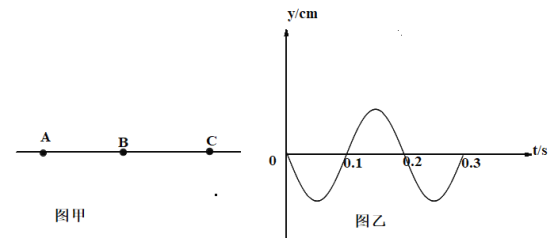
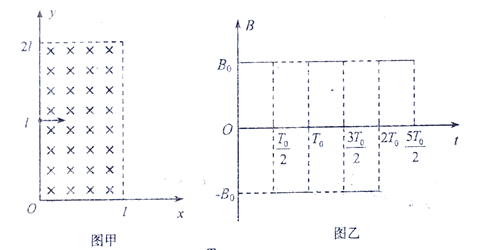
【题目】如图甲所示,平面直角坐标系中,0≤x≤l 、0≤y≤2l的矩形区域中存在交变匀强磁场,规定磁场垂直于纸面向里的方向为正方向,其变化规律如图乙所示,其中B0和T0均未知。比荷为c的带正电的粒子在点(0,![]() )以初速度v0沿+x方向射入磁场,不计粒子重力。
)以初速度v0沿+x方向射入磁场,不计粒子重力。
(1)若在t=0时刻,粒子射入;在t<![]() 的某时刻,粒子从点(l,2l)射出磁场,求B0大小。
的某时刻,粒子从点(l,2l)射出磁场,求B0大小。
(2)若B0=![]() ,且粒子从0≤l≤
,且粒子从0≤l≤![]() 的任一时刻入射时,粒子离开磁场时的位置都不在y轴上,求T0的取值范围。
的任一时刻入射时,粒子离开磁场时的位置都不在y轴上,求T0的取值范围。
(3)若B0= ![]() ,
,![]() ,在x>l的区域施加一个沿-x方向的匀强电场,在
,在x>l的区域施加一个沿-x方向的匀强电场,在![]() 时刻入射的粒子,最终从入射点沿-x方向离开磁场,求电场强度的大小。
时刻入射的粒子,最终从入射点沿-x方向离开磁场,求电场强度的大小。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() .
.
【解析】
设粒子的质量为![]() ,电荷量为
,电荷量为![]() ,则由题意得
,则由题意得
![]()
(1)粒子在磁场中做匀速圆周运动,设运动半径为![]() ,根据几何关系和牛顿第二定律得:
,根据几何关系和牛顿第二定律得:
![]()
![]()
解得![]()
(2)设粒子运动的半径为![]() ,由牛顿第二定律得
,由牛顿第二定律得
![]()
解得![]()
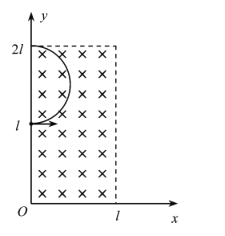
临界情况为:粒子从![]() 时刻射入,并且轨迹恰好过
时刻射入,并且轨迹恰好过![]() 点,粒子才能从
点,粒子才能从![]() 轴射出,如图所示
轴射出,如图所示
设粒子做圆周运动的周期为![]() ,则
,则
![]()
由几何关系可知,在![]() 内,粒子轨迹转过的圆心角为
内,粒子轨迹转过的圆心角为
![]()
对应粒子的运动时间为
![]()
分析可知,只要满足![]() ,就可以使粒子离开磁场时的位置都不在
,就可以使粒子离开磁场时的位置都不在![]() 轴上。
轴上。
联立解得![]() ,即
,即![]() ;
;
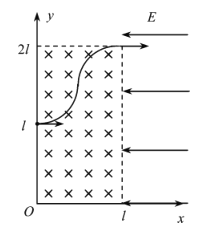
(3)由题意可知,粒子的运动轨迹如图所示
设粒子的运动周期为![]() ,则
,则
![]()
在磁场中,设粒子运动的时间为![]() ,则
,则
![]()
由题意可知,还有
![]()
解得![]() ,即
,即![]()
设电场强度的大小为![]() ,在电场中,设往复一次所用的时间为
,在电场中,设往复一次所用的时间为![]() ,则根据动量定理可得
,则根据动量定理可得
![]()
其中
![]()
![]()
解得![]()
![]()

练习册系列答案
相关题目